Die Auflösung von allgemeinen Dreiecken

Sinussatz:

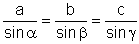a/sin(alpha) = b/sin(beta) = c/sin(gamma)

Cosinussatz:

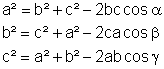a^2 = b^2 + c^2 - 2*b*c*cos(alpha)

Beweis:

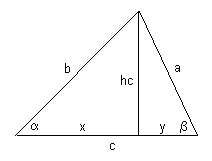
Dreieck mit Höhe h_c

Sinussatz: Wir können die Höhe hc auf zwei Arten ausdrücken:
hc = a·sin β = b·sin α => a/sin α = b/sin β

Cosinussatz:
a² = hc² + y² = (b² - x²) + (c - x)² = b² + c² - 2cx
Wenn wir in diese Gleichung x = b·cos α einsetzen, erhalten wir die angegebene Formel.

Durch zyklisches Vertauschen (a → b, b → c, c → a) erhält man die anderen Gleichungen.

Mit diesen Formeln können wir jedes Dreieck auflösen. Den Sinussatz verwenden wir, wenn eine Seite und der gegenüberliegende Winkel gegeben sind; den Cosinussatz, wenn zwei Seiten und der eingeschlossene Winkel bzw. alle drei Seiten gegeben sind.

Achtung: Die Umkehrung der Sinusfunktion ist für 0° < α < 180° nicht eindeutig (z.B. sin 60° = sin 120°), die Umkehrung der Cosinusfunktion dagegen schon. Wir berechnen daher mit dem Sinussatz im Zweifelsfall immer den kleineren Winkel zuerst, da dieser sicher spitz ist. Wenn die drei Seiten eines Dreiecks gegeben sind, berechnen wir zuerst den größten Winkel (den, der der größten Seite gegenüberliegt) mit Hilfe des Cosinussatzes. Die anderen Winkel kann man dann mit dem (einfacheren) Sinussatz berechnen.

Sind zwei Seiten und der Winkel, der der kleineren Seite gegenüberliegt, gegeben, gibt es zwei Lösungen.

Beispiele:

  1. a = 5, c = 4, α = 30°
    a/sin α = c/sin γ Þ γ = 23,6°
    β = 180° - α - γ = 126,4°
    a/sin α = b/sin β Þ b = 8,0

  2. c = 10, α = 45°, β = 63°
    γ = 180° - α - β = 72°
    a/sin α = c/sin γ Þ a = 7,4
    b/sin β = c/sin γ Þ b = 9,4

  3. b = 4, c = 9, α = 34°
    a² = b² + c² - 2bc cos α Þ a = 6,1
    a/sin α = b/sin β Þ β = 21,5° (kleinerer Winkel)
    γ = 180° - α - β = 124,5°

  4. a = 7, b = 8, c = 5
    b² = a² + c² - 2ac cos β Þ β = 81,8° (größter Winkel)
    b/sin β = c/sin γ Þ γ = 38,2°
    α = 180° - β - γ = 60°

Den Flächeninhalt eines Dreiecks kann man mit der trigonometrischen Flächenformel berechnen:

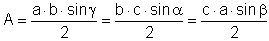A = a*b*sin(gamma)/2

Lernziele:

  • Ich weiß, wann ich den Sinus- bzw. Cosinussatz anwenden kann.
  • Ich kann allgemeine Dreiecke mit Hilfe von Sinus- und Cosinussatz auflösen.

Übungen:
Auflösung von allgemeinen Dreiecken
Vermessungsaufgaben
Flächenberechnungen (Vierecke)
Historische Aufgabe

Zum Inhaltsverzeichnis