Elementare Wahrscheinlichkeitsrechnung
In der Wahrscheinlichkeitsrechnung haben wir es mit Zufallsexperimenten zu tun. Die Wahrscheinlichkeit,
dass das Ereignis A eintritt, bezeichnen wir mit P(A).
Klassische Wahrscheinlichkeitsdefinition nach Laplace:
| P(A) = |
Anzahl der für A günstigen Fälle
Anzahl der möglichen Fälle |
Beispiel: Bei einmaligem Würfeln mit einem fairen Würfel ist P(6) = 1/6.
Rechenregeln:
| 0 ≤ P(A) ≤ 1 |
(das unmögliche Ereignis hat die Wahrscheinlichkeit 0,
das sichere Ereignis die Wahrscheinlichkeit 1) |
P(A oder B) = P(A) + P(B),
wenn A und B einander ausschließen |
z.B.: P(5 oder 6) = 1/6 + 1/6 = 2/6 |
P(A') = 1 - P(A)
(Gegenereignis: A' = "nicht A")
| z.B.: P(nicht 6) = 1 - 1/6 = 5(6)
|
P(A und B) = P(A)·P(B),
wenn A und B voneinander unabhängig sind
| z.B.: bei 2maligem Würfeln ist
P(2mal 6)= 1/6·1/6 = 1/36
|
Beispiele:
-
Wie groß ist die Wahrscheinlichkeit, bei 2maligem Würfeln mindestens 1mal "6" zu werfen?
Wir können die günstigen und möglichen Fälle abzählen (kompliziert) oder so überlegen:
Die Wahrscheinlichkeit für "0mal 6" beträgt 5/6·5/6 = 25/36.
"Mindestens 1mal 6" ist das Gegenereignis dazu, also
P(mind. 1mal 6) = 1 - P(0mal 6) = 1 - 25/36 = 11/36.
Wie oft muss man mindestens würfeln, um mit 90% Wahrscheinlichkeit mindestens 1mal 6 zu
werfen?
Analog zum vorigen Beispiel erhält man bei n-maligem Würfeln
P(mind. 1mal 6) = 1 - (5/6)n
Das soll 90% = 0,9 sein:
1 - (5/6)n = 0,9
Durch Umformen und Logarithmieren erhalten wir
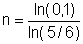 = 12,6
= 12,6
d.h. man muss 13mal würfeln.
Bedingte Wahrscheinlichkeit
Unter der bedingten Wahrscheinlichkeit P(B|A) (B unter der Bedingung A) versteht man die Wahrscheinlichkeit,
dass das Ereignis B eintritt, wenn man bereits weiß, dass das Ereignis A eingetreten ist. Es gilt:
P(B|A) = P(A und B)/P(A)
(Das ist nur eine Abwandlung der Regel "günstige durch mögliche Fälle". Die möglichen
Fälle sind jetzt nur mehr die, die zum Ereignis A gehören.)
Beispiele:
Die Wahrscheinlichkeit, eine 6 zu würfeln unter der Bedingung, dass das Ergebnis
gerade ist, beträgt (1/6)/(1/2) = 1/3.
Ein Spieler hat schon viermal hintereinander eine 6 gewürfelt. Wie groß ist die Wahrscheinlichkeit,
dass beim fünften Wurf wieder eine 6 kommt?
P(5 mal 6|4 mal 6) = (1/6)^5/(1/6)^4 = 1/6, das heißt, die Wahrscheinlichkeit ist von den vorigen Würfen
unabhängig. "Der Würfel hat kein Gedächtnis."
Manche Aufgaben können wir uns mit einem Baumdiagramm veranschaulichen (s.u.).
Die Wahrscheinlichkeiten entlang eines Weges werden multipliziert.
Kann man das gewünschte Ergebnis auf mehrere Arten erhalten, werden die Wahrscheinlichkeiten
für die einzelnen Wege addiert.
Beispiel:
Eine Urne enthält 3 rote und 6 blaue Kugeln. Es wird 3mal je eine Kugel gezogen.
|
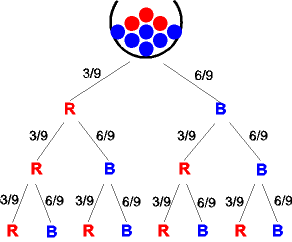
Ziehen mit Zurücklegen:
P(0 mal R) = P(BBB) = 6/9·6/9·6/9 = 8/27 = 0,296
P(1 mal R) = P(RBB) + P(BRB) + P(BBR) =
= 3/9·6/9·6/9 + 6/9·3/9·6/9 + 6/9·6/9·3/9 = 4/9 = 0,444
P(2mal R) = P(RRB) + P(RBR) + P(BRR) =
= 3/9·3/9·6/9 + 3/9·6/9·3/9 + 6/9·3/9·3/9 = 2/9 = 0,222
P(3mal R) = P(RRR) = 3/9·3/9·3/9 = 1/27 = 0,037
|
 |
|
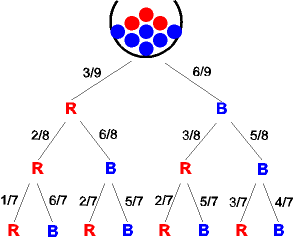
Ziehen ohne Zurücklegen:
P(0 mal R) = P(BBB) = 6/9·5/8·4/7 = 5/21 = 0,238
P(1mal R) = P(RBB) + P(BRB) + P(BBR) =
= 3/9·6/8·5/7 + 6/9·3/8·5/7 + 6/9·5/8·3/7 = 15/28 = 0,536
P(2mal R) = P(RRB) + P(RBR) + P(BRR) =
= 3/9·2/8·6/7 + 3/9·6/8·2/7 + 6/9·3/8·2/7 = 3/14 = 0,214
P(3mal R) = P(RRR) = 3/9·2/8·1/7 = 1/84 = 0,012
|
 |
Lernziele:
- Ich kann einfache Aufgaben mit Baumdiagrammen lösen.
- Ich kann die Mindestanzahl von Versuchen für eine gegebenen Wahrscheinlichkeit berechnen.
|
Übungen
Weiter: Wahrscheinlichkeitsverteilungen
Zum Inhaltsverzeichnis
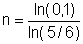 = 12,6
= 12,6
