Diskrete Wahrscheinlichkeitsverteilungen

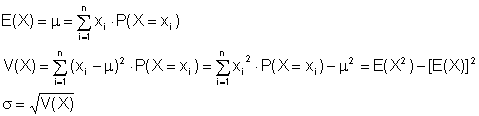
Kann man das Ergebnis eines Zufallsexperiments durch eine Zahl darstellen, so bezeichnet man diese Zahl als Zufallsvariable X. Eine diskrete Zufallsvariable kann nur bestimmte Werte x₁, x₂, ..., x_n annehmen.
Eine Wahrscheinlichkeitsfunktion ordnet jedem Wert x_i die Wahrscheinlichkeit zu, mit der dieser Wert angenommen wird.

Erwartungswert E(X) bzw. μ (my), Varianz V(X) und Standardabweichung σ (sigma) werden analog zur Statistik definiert, wobei die relative Häufigkeit durch die Wahrscheinlichkeit ersetzt wird:

Beispiel:

Im vorigen Beispiel (Ziehen mit Zurücklegen; siehe auch Histogramm) sei X die Anzahl der gezogenen roten Kugeln.

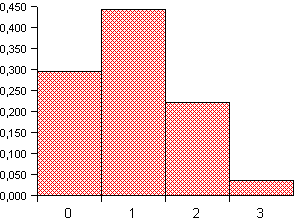
xi	P(X=xi)
0	8/27
1	4/9
2	2/9
3	1/27

μ = 0·8/27 + 1·4/9 + 2·2/9 + 3·1/27 = 1

V(X) = 0²·8/27 + 1²·4/9 + 2²·2/9 + 3²·1/27 - 1² = 2/3

σ = √(2/3) = 0,82

Ebenso erhält man beim Ziehen ohne Zurücklegen:
μ = 1, V(X) = 1/2, σ = 0,71.

Die Binomialverteilung

Eine wichtige Wahrscheinlichkeitsverteilung ist die Binomialverteilung. Sie tritt unter folgenden Bedingungen auf:

• Ein Experiment hat nur zwei mögliche Ausgänge A und A'. Dabei sei P(A) = p und P(A') = q = 1 - p.
• Es kann beliebig oft wiederholt werden.
• Die Wahrscheinlichkeit von A bzw. A' bleibt bei jeder Wiederholung gleich.

(Ein solches Experiment nennt man Bernoulli-Experiment.)

Dann ist die Wahrscheinlichkeit, dass bei n Wiederholungen k-mal das Ereignis A eintritt,

(k = 0, 1, 2, ... n)

(n über k) ist der Binomialkoeffizient.

Für Erwartungswert und Standardabweichung ergeben sich die Formeln

Beispiel:

Wir würfeln 12mal mit einem normalen Würfel, X sei die Anzahl der geworfenen Sechser.
n = 12, p = 1/6, q = 5/6

P(X = 0) = (12 über 0)·(1/6)⁰·(5/6)¹² = 0,112
P(X = 1) = (12 über 1)·(1/6)¹·(5/6)¹¹ = 0,269
P(X = 2) = (12 über 2)·(1/6)²·(5/6)¹⁰ = 0,296

Wahrscheinlichkeit für höchstens 2 Sechser:
P(X £ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0,677

Wahrscheinlichkeit für mindestens 2 Sechser:
P(X ³ 2) = 1 - [P(X = 0) + P(X = 1)] = 0,619

μ = 12·1/6 = 2, σ = √(12·1/6·5/6) = 1,29

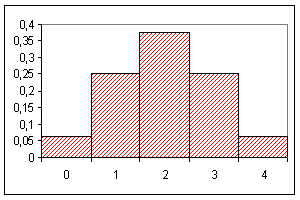
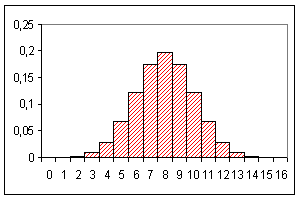
Die beiden Abbildungen zeigen die Binomialverteilung für p = 1/2 und n = 4 bzw. 16. Wie man sieht, nähert sich die Form bei wachsendem n immer mehr einer "Glockenkurve", der Normalverteilung (s. stetige Verteilungen).

Weitere diskrete Wahrscheinlichkeitsverteilungen

Lernziele: Ich kann die Formel für die Binomialverteilung anwenden.

Übungen

Weitere Übungsbeispiele: http://www.zum.de/Faecher/M/NRW/pm/mathe/binvert.htm

Weiter: Stetige Wahrscheinlichkeitsverteilungen

Zum Inhaltsverzeichnis