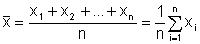
In der Statistik haben wir es mit Stichproben zu tun, die aus einer Grundgesamtheit (alle Einwohner eines Landes, alle Äpfel aus einer Lieferung ...) entnommen werden. Die Elemente der Stichprobe werden auf ein bestimmtes Merkmal untersucht, das in verschiedenen Ausprägungen auftreten kann.
n: Umfang der Stichprobe
x1, x2, ..., xn: gemessene Werte (Ausprägungen des untersuchten Merkmals)
H1, H2, ... : absolute Häufigkeit
h1, h2, ...:relative Häufigkeit (hi = Hi/n)
Je nach Art eines Merkmals unterscheidet man verschiedene Skalenniveaus:
Nominalskala: verschiedene Eigenschaften, keine vorgegebene Reihenfolge (z.B. Geschlecht, Wohnort)
Ordinalskala: die Werte können geordnet werden, man kann aber keine Abstände zwischen ihnen angeben (z.B. Rangplätze, Schulnoten)
Intervallskala: der Abstand zwischen zwei Werten lässt sich messen, der Nullpunkt ist willkürlich festgelegt (z.B. Jahreszahlen, Temperatur in °C)
Verhältnisskala: es gibt einen natürlichen Nullpunkt, man kann also sowohl die Differenz als auch das Verhältnis zweier Werte angeben (z.B. Alter, Einkommen). Solche Daten liefern die meiste Information.
Die Häufigkeiten stellt man gern in einem Histogramm dar (siehe Beispiel).
Bei großen Datenmengen teilt man die Werte in Klassen ein (z.B. Größe 150 - 160 cm, 160 - 170 cm ...)
Wir versuchen, die Stichprobe durch einen "mittleren Wert" zu beschreiben.
MittelwertDer Mittelwert (das arithmetische Mittel) ist das wichtigste Zentralmaß:
(Zur Verwendung des Summenzeichens)
Wenn Werte mehrmals vorkommen, rechnet man besser mit den relativen Häufigkeiten:
(gewichtetes arithmetisches Mittel)
Bei klassifizierten Daten verwendet man die Klassenmitten als Messwerte (z.B. Körpergröße 150 - 160 cm: wir rechnen mit xi = 155 cm). Der Mittelwert ist nur bei intervall- und verhältnisskalierten Daten sinnvoll.
Median:
Das arithmetische Mittel hat den Nachteil, dass es sehr empfindlich gegenüber "Ausreißern" ist (wenn z.B. in einer Firma 9 Personen je 1000 € verdienen und der Chef 11000 €, beträgt das "Durchschnittseinkommen" 2000 €!) In solchen Fällen ist der Median (Zentralwert) aussagekräftiger: Wir ordnen die Daten der Größe nach und betrachten den Wert in der Mitte der Liste. Bei einer geraden Anzahl von Daten bilden wir das arithmetische Mittel der beiden mittleren Werte. Die so erhaltene Zahl hat die Eigenschaft, dass die Hälfte der Werte darunter, die Hälfte darüber liegt.
= x(n+1)/2
für ungerades n = 1/2(xn/2 + xn/2+1)
für gerades n (xi: Werte aus geordneter Urliste)
Der Median kann bei ordinal-, intervall- und verhältnisskalierten Daten angewendet werden.
Modus
Der Modus (Modalwert) ist der Wert, der am häufigsten vorkommt. Eine Stichprobe kann auch mehrere Modalwerte haben. Dieser Wert liefert am wenigsten Information, er kann aber auf allen Datenniveaus angewendet werden.
liefern ein Maß dafür, wie sehr die gemessenen Werte vom Mittelwert abweichen.
Varianz und Standardabweichung
Wir interessieren uns für die Differenzen der gemessenen Werte zum Mittelwert. Damit wir nicht mit negativen Zahlen rechnen müssen, quadrieren wir diese Differenzen und bilden davon wieder den Mittelwert. So erhalten wir die Varianz:
Das kann man umformen zu folgender Formel, die leichter zu berechnen ist:
("Mittelwert der Quadrate minus Quadrat des Mittelwerts")
Wenn Werte mehrmals vorkommen, rechnet man wieder mit dem gewichteten Mittel:
Damit die Dimension wieder "stimmt", ziehen wir die Wurzel aus der Varianz und erhalten die Standardabweichung: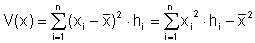
(Achtung, Verwechslungsgefahr:
In manchen Büchern findet sich für die Varianz folgende Formel:
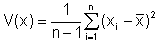
Sie wird dann verwendet, wenn man aufgrund einer Stichprobe die Varianz der Grundgesamtheit abschätzen will.)
Spannweite
Die Differenz zwischen dem kleinstem und dem größten Wert bezeichnet man als Spannweite (engl. range). Dieses Streuungsmaß ist besonders leicht zu berechnen.
R = xmax - xmin
Quartile:
Die Quartile definiert man analog zum Median:
unteres Quartil Q1 bzw. Q0,25: ¼ der Werte liegen darunter
oberes Quartil Q3 bzw. Q0,75: ¾ der Werte liegen darunter
Der Median ist in dieser Bezeichnungsweise das 2. Quartil Q2 bzw. Q0,5.
(Ebenso definiert man Perzentile, z.B. 10%-Perzentil Q0,1: 10% der Werte liegen darunter.)
Eine sehr übersichtliche Darstellung von Median, Spannweite und Quartilen ist das Boxplot-Diagramm ("box and whiskers", siehe Beispiel): Die "Box" reicht vom unteren bis zum oberen Quartil, die Linie in der Mitte gibt den Median an. Der "Schnurrbart" reicht bis zum kleinsten bzw. größten Wert.
Beispiel:
Zehn Frauen wurden nach ihrer Körpergröße (in cm) gefragt.
Urliste:
168, 170, 161, 168, 162, 172, 164, 167, 170, 158
Geordnete Urliste:
158, 161, 162, 164, 167, 168, 168, 170, 170, 172
Mittelwert:
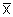 = (158+161+162+164+167+168+168+170+170+172)/10 = 166
= (158+161+162+164+167+168+168+170+170+172)/10 = 166
Median: 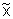 = (167+168)/2 = 167,5
= (167+168)/2 = 167,5
Modi: 168 und 170
Varianz und Standardabweichung:
V(x) = (158²+161²+162²+164²+167²+168²+168²+170²+170²+172²)/10 - 166² = 18,6
s = √18,6 = 4,313
Spannweite: R = 172 - 158 = 14
Quartile:
Q1 = 162 (liegt in der Mitte der unteren Hälfte)
Q3 = 170 (liegt in der Mitte der oberen Hälfte)
(Anmerkung: Die Berechnung der Quartile ist nicht ganz einheitlich; hier wurde offensichtlich nach einer etwas anderen Vorschrift gerechnet.)
Dieselben Frauen gaben auch ihre Schuhgröße an.
Urliste:
39, 39, 38, 38, 37, 41, 38, 38, 40, 37
Hier rechnen wir besser mit den relativen Häufigkeiten:
Schuhgröße |
Hi |
hi |
37 |
2 |
0,2 |
38 |
4 |
0,4 |
39 |
2 |
0,2 |
40 |
1 |
0,1 |
41 |
1 |
0,1 |
Mittelwert:
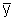 = 37·0,2 + 38·0,4 + 39·0,2 +
40·0,1 + 41·0,1 = 38,5
= 37·0,2 + 38·0,4 + 39·0,2 +
40·0,1 + 41·0,1 = 38,5
Median: 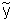 = 38
= 38
Modus: 38
Varianz und Standardabweichung:
V(y) = 37²·0,2 + 38²·0,4 + 39²·0,2 + 40²·0,1 + 41²·0,1 -
38,5² = 1,45
s = √11,45 = 1,204
Spannweite: R = 41 - 37 = 4
Quartile: Q1 = 38, Q3 = 39
Links:
http://medweb.uni-muenster.de/institute/imib/lehre/skripte/biomathe/jumbo.html:
ausführliches Skriptum der Universität Münster, mit vielen Java-Applets
Weiter: Lineare Regression