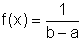für a ≤ x ≤ b, sonst 0
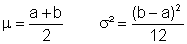
Gleichverteilung
Eine stetige Zufallsvariable ist gleichverteilt, wenn sie in einem bestimmten Intervall jeden Wert mit derselben Wahrscheinlichkeit annehmen kann. Ihre Dichtefunktion lautet:
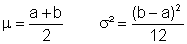
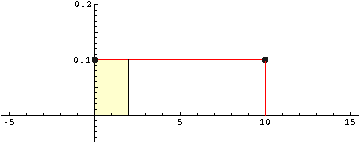
Beispiel: Ein Bus fährt in regelmäßigen Abständen von 10 Minuten. Wie groß ist die Wahrscheinlichkeit, dass ich höchstens 2 Minuten warten muss, wenn ich zu einem beliebigen Zeitpunkt zur Haltestelle komme?
Die Wartezeit ist gleichverteilt im Intervall [0; 10]. Wir erhalten daher:
P(X ≤ 2) = 2·0,1 = 0,2
Exponentialverteilung
Diese Verteilung ist die stetige Entsprechung zur geometrischen Verteilung. Sie hängt auch mit der Poisson-Verteilung zusammen: Bei einem Poisson-Prozess der Dichte λ ist die Wartezeit zwischen zwei aufeinanderfolgenden Ereignissen exponentialverteilt. Ihre Dichtefunktion lautet:
f(x) = l·e-lx für x ≥ 0, sonst 0
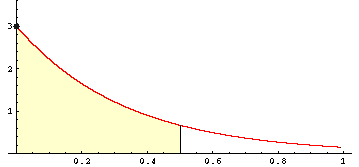
Beispiel: Die Bibliothekarin (aus dem Beispiel zur Poisson-Verteilung) möchte gerne Pause machen. Wie groß ist die Wahrscheinlichkeit, dass der nächste Benutzer innerhalb der nächsten halben Stunde kommt?
In diesem Beispiel war λ = 3. Wir erhalten daher mit Hilfe der Integralrechnung:
