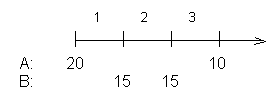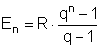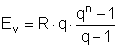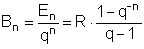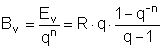Zins-, Zinseszins- und Rentenrechnung
Wenn ein Kapital für einen gewissen Zeitraum ausgeliehen wird, muss man dafür
Zinsen zahlen. Es gibt verschiedene Möglichkeiten, die Zinsen zu berechnen:
- Einfache (lineare) Verzinsung:
Die Zinsen werden für die gesamte Laufzeit berechnet (proportional zur Laufzeit).
- Zinseszinsen (exponentielle Verzinsung):
Nach jeder Zinsperiode (z.B. am Ende des Jahres) werden die aufgelaufenen Zinsen dem
Kapital zugeschlagen und tragen von da an selbst wieder Zinsen.
- Dekursive Verzinsung:
Die Zinsen werden vom Anfangskapital berechnet und dem Kapital am Ende der Laufzeit
(bzw. Zinsperiode) zugeschlagen
- Antizipative Verzinsung:
Die Zinsen (Diskont) werden vom Endkapital berechnet und am Beginn der Laufzeit gezahlt.
Bezeichnungen:
| K0: | Barwert (Anfangskapital) |
| Kn: | Endwert (Kapital nach n Jahren) |
| i: | Zinssatz (interest rate) |
| d: | Diskontsatz (discount rate) |
| n: | Laufzeit |
Wir geben Zinssatz und Diskontsatz in Prozent oder als Dezimalzahl an, z.B.
i = 5% = 0,05.
Einfache Verzinsung
dekursiv:
Ein Kapital K0 wird n Jahre zum Jahreszinssatz i angelegt. Die Zinsen
betragen K0·n·i, das Endkapital ist daher
Wir erhalten also eine lineare Funktion der Zeit.
Die einfache Verzinsung wird nur für Zeiträume unter 1 Jahr angewendet.
Beispiele:
- 400 € werden 5 Monate zum Zinssatz i = 6% angelegt.
Kn = 400·(1 + 5/12·0,06) = 410 €
- Welchen Betrag muss man auf ein Sparbuch mit 4% Verzinsung einzahlen, wenn man in
9 Monaten 800 € abheben will?
800 = K0·(1 + 9/12·0,04) = K0·1,03
⇒ K0 = 800/1,03 = 776,70 €
antizipativ:
Diese Art der Verzinsung wird vor allem bei der Wechseldiskontierung angewendet.
Mit einem Wechsel verpflichtet man sich, zu einem späteren Zeitpunkt einen bestimmten Betrag
Kn zu zahlen. Wenn der Empfänger des Wechsels ihn schon früher einlösen will,
erhält er von der Bank den um die Diskontzinsen verminderten Betrag. Die Zinsen betragen
Kn·n·d, der Auszahlungbetrag K0 ist daher
Auch die lineare antizipative Verzinsung wird nur für Zeiträume unter 1 Jahr angewendet.
Sie hat heute keine große praktische Bedeutung mehr.
Beispiele:
- Ein Wechsel, der auf den Betrag Kn = 500 € lautet, wird 2 Monate
vor seiner Fälligkeit eingelöst. Welche Summe wird ausgezahlt, wenn die Bank d = 6%
Diskontzinsen berechnet?
K0 = 500·(1 - 2/12·0,06) = 495 €
- Eine Rechnung lautet auf den Betrag K0 = 790 €.
Ein Geschäftsmann will sie durch einen Wechsel begleichen, der in 3 Monaten fällig ist.
Auf welchen Betrag muss er den Wechsel ausstellen, wenn 5% Diskontzinsen berechnet werden?
790 = Kn·(1 - 3/12·0,05) = Kn·0,9875
⇒ Kn = 790/0,9875 = 800 €
- Jemand leiht sich 1000 € ein Jahr lang zum Diskontsatz d = 10% aus. Welcher dekursive
Zinssatz wäre dazu äquivalent?
Kn = 1000/(1 - 0,1) = 1111,11
Das entspricht einer dekursiven Verzinsung von i ≈ 11%.
Wie wir am letzten Beispiel sehen, sind ein bestimmter Zinssatz und ein nominell
gleich hoher Diskontsatz nicht äquivalent.
Zinseszinsen
Die angelaufenen Zinsen werden am Ende jeder Zinsperiode dem Kapital hinzugefügt.
(Wir betrachten hier nur dekursive Verzinsung.) Das Kapital wächst also pro Jahr
umd den Aufzinsungsfaktor q = 1 + i, und der Endwert beträgt
| Kn = K0·qn, wobei q = 1 + i |
Das Endkapital hängt also exponentiell von der Zeit ab.
Beispiele:
- Auf welchen Betrag wächst ein Kapital von 100 € in 8 Jahren
bei einer Verzinsung von i = 5%?
Kn = 100·1,058 = 147,75 €
- Wie hoch war ein Kapital, wenn es in 5 Jahren bei einer Verzinsung von i = 3% auf 742
€ angewachsen ist?
742 = K0·1,035 ⇒
K0 = 742/1,035 = 640 €
- Jemand leiht sich 4000 € aus und zahlt nach 4 Jahren 4500 € zurück.
Welchem Zinsatz entspricht das?
4500 = 4000·q4 ⇒
q =
4√(4500/4000) ≈ 1,03,
i ≈ 3%
Wie lange dauert es, bis ein Kapital von 1500 € bei einer Verzinsung von 4,5% auf 2000
€ anwächst?
2000 = 1500·1,045n ⇒
n = log(2000/1500)/log(1,045) ≈ 6,5 Jahre
Das Äquivalenzprinzip der Finanzmathematik
Zahlungen dürfen nur dann verglichen / addiert / subtrahiert werden,
wenn sie zuvor auf denselben Stichtag auf- oder abgezinst wurden!
Beispiel:
Für eine Immobilie liegen zwei Angebote vor: A bietet 20000 € sofort und 10000 €
in 3 Jahren; B bietet je 15000 € in einem Jahr und in 2 Jahren. Welches Angebot ist -
bei einer Verzinsung von 5% - für den Verkäufer günstiger?
Solche Aufgaben veranschaulicht man am besten durch einen Zeitstrahl:
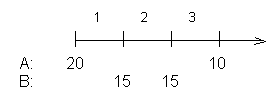
Wir können beispielsweise alle Zahlungen auf das Ende des 3. Jahres aufzinsen:
A: 20000·1,053 + 10000 = 33152,50
B: 15000·1,052 + 15000·1,05 = 32287,50
Angebot A ist also für den Verkäufer etwas günstiger.
(Dasselbe Ergebnis hätten wir erhalten, wenn wir einen anderen Bezugszeitpunkt, z.B.
den Anfang des 1. Jahres, gewählt hätten.)
Unterjährige Verzinsung
Oft werden die Zinsen mehrmals pro Jahr dem Kapital zugeschlagen (halbjährlich, vierteljährlich
oder monatlich). Für die Berechnung des unterjährigen Zinssatzes im (m ist die
Anzahl der Zinsperioden pro Jahr) gibt es zwei Möglichkeiten:
Relativer unterjähriger Zinssatz: im = i/m
Der nominelle Jahreszinssatz wird durch die Anzahl der Zinsperioden geteilt.
Dabei ergibt sich allerdings ein höherer Effektivzinsatz.
Bsp.: K0 = 100, i = 12%, n = 1
| halbjährlich: |
i2 = 6% |
K1 = 100·1,062 = 112,36 |
ieff = 12,36% |
| vierteljährlich: |
i4 = 3% |
K1 = 100·1,034 = 112,55 |
ieff = 12,55% |
| monatlich: |
i12 = 1% |
K1 = 100·1,0112 = 112,68 |
ieff = 12,68% |
Konformer (äquivalenter) unterjähriger Zinssatz:
im wird so bestimmt, dass sich derselbe Effektivzinssatz ergibt wie bei jährlicher
Verzinsung.
Betrachten wir wieder das Beispiel i = 12%:
| halbjährlich: |
(1 + i2)2 = 1,12 |
i2 = 5,83% |
| vierteljährlich: |
(1 + i4)4 = 1,12 |
i4 = 2,87% |
| monatlich: |
(1 + i12)12 = 1,12 |
i12 = 0,95% |
Man kommt also nur zu widerspruchsfreien Ergebnissen, wenn man den konformen
unterjährigen Zinssatz verwendet!
Exkurs: Stetige Verzinsung
Wenn man (bei gleichbleibendem nominellen Zinssatz) die Anzahl der Zinsperioden vergrößert,
wird das Endkapital immer größer. Es gibt aber eine obere Grenze.
Setzen wir der Einfachheit halber K0 = 1, i = 100%:
| m | K1 |
| 1 | 1 + 1 = 2 |
| 2 | (1 + ½)2 = 2,25 |
| 4 | (1 + ¼)4 = 2,441 |
| 12 | (1 + 1/12)12 = 2,613 |
| 100 | (1 + 1/100)100 = 2,705 |
| 1000 | (1 + 1/1000)1000 = 2,717 |
Der Grenzwert dieser Folge für m → ∞ ist die
Euler'sche Zahl e = 2,71828...
Allgemein: Endwert eines Kapitals bei stetiger Verzinsung zum nominellen Zinssatz i:
Kn = K0·ei·n
Die stetige Verzinsung eines Kapitals ist in der Praxis nicht durchführbar; sie stellt
aber ein gutes Modell für natürliche Vorgänge (Wachstumsvorgänge,
radioaktiver Zerfall u.a.) dar.
Rentenrechnung
Eine Reihe von gleichhohen Zahlungen (Raten) in regelmäßigen Zeitabständen bezeichnet man als
Rente.
Bezeichnungen:
R: Rate
E: Endwert (Wert am Ende des Rentenzeitraums)
B: Barwert (Wert am Beginn des Rentenzeitraums)
Rentenperiode: Zeitraum zwischen zwei Raten
Nachschüssige Rente: Zahlungen am Ende jeder Rentenperiode
Vorschüssige Rente: Zahlungen am Beginn jeder Rentenperiode
Wir nehmen zunächst an, dass Rentenperiode und Zinsperiode übereinstimmen,
und bestimmen den Endwert einer n-maligen, nachschüssigen Rente. (Die Rentenperiode sei ein Jahr.)
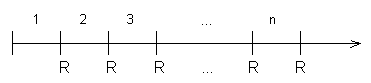
Wir zinsen alle Raten, beginnend mit der letzten, auf den Tag der letzten Zahlung
auf:
En = R + R·q + R·q2 + ... + R·qn-1 =
R·(1 + q + q2 + ... + qn-1)
Beweis:
Der Ausdruck in der Klammer ist eine geometrische Reihe. Wir bezeichnen die Summe
mit sn:
| |
sn = 1 + q + q2 + ... + qn-1 |
| Beide Seiten mit q multiplizieren: |
q·sn = q + q2 + ... + qn-1 + qn |
| Obere Gleichung von unterer abziehen: |
sn·(q - 1) = qn - 1
sn = (qn - 1)/(q - 1) |
Um den Endwert einer vorschüssigen Rente zu erhalten, muss man diesen Betrag noch durch ein Jahr
aufzinsen, weil das Ende des Rentenzeitraums ein Jahr nach der letzten Zahlung liegt.
Den Barwert erhält man, indem man den Endwert durch n Jahre abzinst. Daher ergeben sich
folgende Formeln:
| |
nachschüssig |
vorschüssig |
| Endwert: |
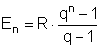
|
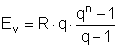
|
| Barwert: |
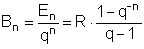
|
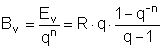
|
Wenn Rentenperiode und Zinsperiode nicht gleich lang sind, muss man mit dem
äquivalenten Zinssatz rechnen, z.B.:
monatliche Zahlungen, Jahreszinssatz i = 5%: q = 12√1,05
= 1,0041
zweijährige Zahlungen, Jahreszinssatz i = 5%: q = 1,052 = 1,1025
Beispiele:
Herr A. zahlt 15 Jahre lang am Ende jedes Jahres 1000 € ein (i = 4%). Von dem ersparten
Geld will er 20 vorschüssige Jahresraten beheben, beginnend 5 Jahre nach der letzten Einzahlung.
Wie hoch ist eine Rate?
Wert 5 Jahre nach der letzten Einzahlung: Endwert (nachschüssig), aufgezinst durch 5 Jahre
1000·(1,0415 - 1)/0,04·1,045 = 24361,76
Das ist der Barwert der neuen Rente (vorschüssig):
24361,76 = R·1,04·(1 - 1,04-20)/0,04 ⇒
R = 1723,64
Frau B. nimmt einen Kredit von 15000 € mit einer Laufzeit von 10 Jahren auf,
den sie in nachschüssigen Monatsraten zurückzahlen will (i = 8%). Wie hoch ist eine Rate?
Nach 3 Jahren erhöht die Bank den Zinssatz auf 10%. Um wieviel verlängert sich die Laufzeit, wenn
Frau B. die Raten in derselben Höhe weiterzahlt?
Den Aufzinsungsfaktor erhalten wir aus dem konformen Monatszinssatz:
q = 1 + i12 = 12
√1,08 = 1,0064
Die Kreditsumme ist der Barwert, es sind 120 nachschüssige Raten zu zahlen:
15000 = R·(1 - 1,0064-120)/0,0064 ⇒
R = 179,79
Restschuld nach 3 Jahren: Kreditsumme, aufgezinst durch 3 Jahre, minus Endwert der Raten
nach 36 Monaten:
15000·1,083 - 179,79·(1,006436 - 1)/0,0064 = 11638,54
Das ist der neue Barwert; der neue Aufzinsungsfaktor beträgt 12√1,1
= 1,008
11638,54 = 179,79·(1 - 1,008-n)/0,008
1,008-n = 0,4838
n = -log(0,4838)/log(1,008) = 91,4
Die Laufzeit verlängert sich um (91,4 - 84 =) 7,4 Monate.
(Bei solchen Aufgaben empfiehlt es sich, q im Speicher des Taschenrechners zu speichern.)
Übungen
Zum Inhaltsverzeichnis