Nr. 19 / Juni 2007
Hallo!
Nach dem Aprilscherz vom letzten Mal möchte ich diesmal wieder vor allem für meine ursprüngliche Zielgruppe schreiben: ehemalige Kursteilnehmer und Leute mit Schulkenntnissen in Mathematik. Für die Spezialisten unter euch wird also nicht viel Neues dabei sein. Ich möchte ein Thema behandeln, das ich schon in verschiedenen Zusammenhängen kurz gestreift habe:
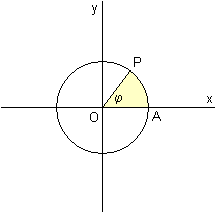
Ein Punkt P auf dem Einheitskreis x² + y² = 1 hat die Koordinaten x = cos(φ), y = sin(φ). φ ist dabei der Winkel zwischen OP und der x-Achse. Wenn man im Bogenmaß rechnet, hat der Kreisbogen AP die Länge φ und der Kreissektor OAP den Flächeninhalt φ/2.
|
|
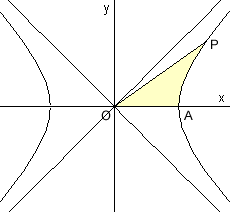
Der italienische Jesuit Vincenzo Riccati (1710 - 1775) wollte auch für die gleichseitige Hyperbel x² - y² = 1 eine ähnliche Darstellung finden. Er wählte dabei den Flächeninhalt des Hyperbelsektors OAP als Parameter. Ich werde seinen Beweis nur ganz kurz in heutiger Schreibweise skizzieren.
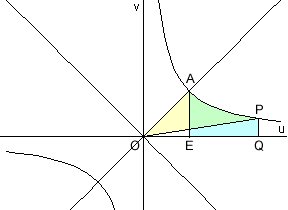
Wenn wir die Hyperbel um 45° drehen, erhalten wir ein neues Koordinatensystem (u,v) mit den Asymptoten als Achsen. Wenn man einen passenden Maßstab wählt, hat die Kurve in diesem Koordinatensystem die Gleichung uv = 1 bzw. v = 1/u. Die Dreiecke OAE und OPQ sind daher gleich groß. Also hat der Sektor OAP denselben Flächeninhalt wie das Flächenstück APEQ (man muss nur das Dreieck OPQ dazufügen und das gleich große Dreieck OAE abziehen). Diese Fläche ist aber das Integral von 1/u, das heißt, der natürliche Logarithmus von u (oder, wie man damals auch sagte, der hyperbolische Logarithmus). Bezeichnen wir den Flächeninhalt mit t, so ist u = et und v = 1/u = e-t. Wenn wir die Hyperbel wieder zurückdrehen und den Maßstab richtig anpassen, erhalten wir
(Genau genommen ist der Flächeninhalt des Sektors t/2, so wie beim Kreis.) Wegen der Analogie zu den Winkelfunktionen nannte Riccati diese Funktionen Sinus hyperbolicus (sinh) und Cosinus hyperbolicus (cosh). Er führte auch den Tangens hyperbolicus durch die Gleichung tanh(x) = sinh(x)/cosh(x) ein. Heute definiert man einfach:
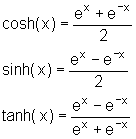 |
Aus der Gleichung der Hyperbel leitete Riccati ab: cosh²(x) - sinh²(x) = 1. Das erinnert an die Beziehung cos²(x) + sin²(x) = 1. Man kann die Formel einfach nachrechnen, indem man die Definitionen einsetzt. Es gibt noch andere Parallelen zwischen den Winkel- und Hyperbelfunktionen, obwohl ihre Graphen ganz verschieden aussehen, z.B.:
| cos²(x) + sin²(x) = 1 | cosh²(x) - sinh(²(x) = 1 |
| (sin(x))' = cos(x) | (sinh(x))' = cosh(x) |
| (cos(x))' = -sin(x) | (cosh(x))' = sinh(x) |
| (tan(x))' = 1 + tan²(x) | (tanh(x))' = 1 - tanh²(x) |
| sin(x + y) = sin(x)cos(y) + cos(x)sin(y) | sinh(x + y) = sinh(x)cosh(y) + cosh(x)sinh(y) |
| cos(x + y) = cos(x)cos(y) - sin(x)sin(y) | cosh(x + y) = cosh(x)cosh(y) + sinh(x)sinh(y) |
Die Graphen von sin (blau), cos (rot) und tan (grün) |
Die Graphen von sinh (blau), cosh (rot) und tanh (grün) |
Der wichtigste Unterschied besteht darin, dass die Winkelfunktionen periodisch sind, die Hyperbelfunktionen aber nicht.
Auf eine dieser Funktionen waren die Mathematiker schon viel früher gestoßen. Ende des 17.Jahrhunderts waren die besten Mathematiker damit beschäftigt, die neu entdeckte Differentialrechnung auf verschiedenste Probleme anzuwenden. Oft stellten sie sich gegenseitig Aufgaben zur Herausforderung, unter anderem in der von Gottfried W. Leibniz gegründeten Zeitschrift Acta eruditorum. 1690 stellte Jakob Bernoulli dort folgendes Problem zur Diskussion: Welche Form nimmt eine Kette an, die an ihren beiden Endpunkten aufgehängt ist? Galilei hatte angenommen, dass diese Kurve eine Parabel sei. Das stellte sich aber als falsch heraus. Leibniz, Christiaan Huygens und Jakobs Bruder Johann Bernoulli fanden unabhängig voneinander die Lösung: Die gesuchte Kurve ist der Graph der hyperbolischen Cosinusfunktion, die allerdings damals noch nicht unter diesem Namen bekannt war. Sie gaben auch nicht einfach die Funktionsgleichung an, sondern geometrische Konstruktionsvorschriften für Kurve und Tangente, die uns heute ziemlich kompliziert vorkommen (im Bild links die Lösung von Leibniz). Heute kann man diese Kurve (fast) mit Methoden der Schulmathematik behandeln.
|
Übrigens: wenn die Kettenlinie um die x-Achse rotiert, entsteht ein sogenanntes Katenoid. Diese Fläche hat überall die mittlere Krümmung 0 und wird auch als Minimalfläche bezeichnet, weil eine gespannte Membran, z.B. eine Seifenhaut, eine solche Form annehmen kann. Man kann sie also erhalten, indem man zwei Drahtringe in Seifenlösung taucht und dann vorsichtig auseinanderzieht (Bild rechts).
Bekanntlich ist der Graph einer Polynomfunktion, bei der nur gerade Potenzen von x vorkommen, symmetrisch zur y-Achse. Eine solche Funktion heißt auch gerade Funktion (f(-x) = f(x)). Wenn nur ungerade Hochzahlen vorkommen, ist der Graph symmetrisch zum Koordinatenursprung; man spricht von einer ungeraden Funktion (f(-x) = -f(x)). Eine beliebige Polynomfunktion kann man in einen geraden und ungeraden Anteil zerlegen. So ist z.B. die Funktion f(x) = x³ + 3x² - 9x - 27 die Summe der geraden Funktion fg(x) = 3x² - 27 und der ungeraden Funktion fu(x) = x³ - 9x.
Diese Idee können wir auf beliebige Funktionen verallgemeinern. Zu einer Funktion f(x) definieren wir
Man kann leicht überprüfen, dass der Wert von fg gleich bleibt, wenn man x durch -x ersetzt; bei fu ändert sich das Vorzeichen. Wenn man die beiden Funktionen addiert, erhält man wieder die ursprüngliche Funktion f(x). Man kann also jede Funktion, die auf ganz R definiert ist, als Summe einer geraden und einer ungeraden Funktion darstellen. Wenn man von der Funktion f(x) = ex ausgeht, erhät man die Funktionen fg(x) = cosh(x), fu(x) = sinh(x). Wir können diese Funktionen also einfach als geraden und ungeraden Anteil der natürlichen Exponentialfunktion auffassen.
Man kann diese Funktion auch als unendliche Reihe darstellen:
Wenn man die geraden und ungeraden Potenzen trennt, erhält man für die Hyperbelfunktionen die Reihen
Die Darstellung der Cosinus- und Sinusfunktion als unendliche Reihe lautet
Auch hier besteht offensichtlich wieder eine Ähnlichkeit.
Dass diese Parallelen nicht nur zufällig sind, erkennt man erst, wenn man auch komplexe Zahlen betrachtet. Aus der Eulerschen Formel
eiφ = cos(φ) + i·sin(φ)
erhält man die Gleichungen
die man auch zur Definition der Winkelfunktionen benutzen kann. (Dazu muss man natürlich vorher erklärt haben, was e hoch einer imaginären Zahl bedeutet.) Hier ist die Ähnlichkeit unübersehbar. Setzt man in diesen Gleichungen φ = ix und formt ein bisschen um, so ergeben sich die Beziehungen
cos(ix) = cosh(x)
sin(ix) = i·sinh(x)
Von der höheren Ebene der komplexen Zahlen aus betrachtet, sind also Winkelfunktionen und Hyperbelfunktionen nur zwei verschiedene Schreibweisen für dieselbe Sache. Beide gehören zur großen Gruppe der Exponentialfunktionen.
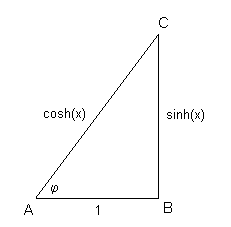 Es gibt noch einen anderen Zusammenhang zwischen Winkel- und Hyperbelfunktionen, der ohne komplexe Zahlen auskommt.
Wegen der Beziehung cosh²(x) - sinh²(x) = 1 kann man für jeden Wert von x ein rechtwinkeliges Dreieck mit den
Seitenlängen 1, sinh(x) und cosh(x) zeichnen. Für den Winkel φ in diesem Dreieck gilt dann
Es gibt noch einen anderen Zusammenhang zwischen Winkel- und Hyperbelfunktionen, der ohne komplexe Zahlen auskommt.
Wegen der Beziehung cosh²(x) - sinh²(x) = 1 kann man für jeden Wert von x ein rechtwinkeliges Dreieck mit den
Seitenlängen 1, sinh(x) und cosh(x) zeichnen. Für den Winkel φ in diesem Dreieck gilt dann
tan(φ) = sinh(x)
cos(φ) = 1/cosh(x)
sin(φ) = sinh(x)/cosh(x) = tanh(x)
Dadurch wird jeder reellen Zahl x ein Winkel zwischen -90° und 90° zugeordnet. Diese Zuordnung heißt Gudermannfunktion φ = gd(x) (nach Christoph Gudermann (1798 - 1852), einem Schüler von Gauss). Sie kann noch auf viele andere Arten dargestellt werden. Mit ihrer Hilfe kann man zum Beispiel die Gleichung der Kettenlinie (Coxeter S. 318), die Mercatorkarte1 (s. Mathe-Newsletter 10) und den Parallelwinkel in der hyperbolischen Geometrie2 (s. Mathe-Newsletter 11) berechnen.
Vielleicht habe ich euch Lust gemacht, zu diesem Thema ein bisschen weiter zu forschen. Ihr werdet sehen, dass es da noch eine Unmenge zu entdecken gibt!
Einen schönen Sommer wünscht euch
Jutta
1: Ein Punkt, der auf der Mercatorkarte den Abstand h vom Äquator hat, liegt in Wirklichkeit auf der geographischen Breite φ = gd(h). Wenn h aus der geographischen Breite berechnet werden soll, braucht man also die Umkehrfunktion.
2: In der hyperbolischen Geometrie gibt es - anders als in der euklidischen - durch einen Punkt P mehrere Parallelen zu einer Geraden g. Der Parallelwinkel (der Mindestwinkel, den diese Parallelen mit der Normalen Pg einschließen), hängt vom Abstand a = Pg ab. Er beträgt Π(a) = 90° - gd(a).
Maor, Eli: Die Zahl e - Geschichte und Geschichten, Basel 1996
Coxeter, H. S. M.: Introduction to Geometry, 2nd Ed., Hoboken, NJ 1989
Website über Hyperbelfunktionen: http://www.mathe-online.at/materialien/Thomas/files/hyperbel.html
Projekte zur Kettenlinie:
http://teacher.eduhi.at/alindner/Dyn_Geometrie/kettenlinie/
http://mathsrv.ku-eichstaett.de/MGF/homes/grothmann/Projekte/Kettenlinie/index.html
http://www.arndt-bruenner.de/mathe/java/kettenlinie.htm
Wikipedia-Artikel:
Hyperbelfunktionen: http://de.wikipedia.org/wiki/Hyperbelfunktionen
Kettenlinie: http://de.wikipedia.org/wiki/Katenoide
Gudermannfunktion: http://de.wikipedia.org/wiki/Gudermannfunktion
Seite über Riccati (englisch): http://www.faculty.fairfield.edu/jmac/sj/scientists/riccati.htm
Links zu Minimalflächen: http://www.mathematik.uni-kassel.de/~rascha/MathWWW_Minimalflaechen.htm
E-mail: gut.jutta.gerhard@chello.at