TI-92: MODERNES HILFSMITTEL IN DER MATHEMATIK
verfasst von Dr. Manfred
Gurtner-Würl
Hier ein LINK zur Erklärung vom VOYAGE200: VOYAGE 200

Übersicht über die Hilfsmittel in
der Mathematik
Seit ca. 1970 gibt es
Taschenrechner (TR). Die Einführung des Taschenrechners in den Schulen führte
zu einer Neuorientierung der Mathematik. Davor waren die Beispiele stark auf
das Kopfrechnen und das schriftliche Rechnen fixiert, Funktionswerte mussten in
einer Tabelle nachgeschlagen werden oder am Rechenschieber gesucht werden.
Danach wurden grafische Taschenrechner erfunden, die Funktionen auf Knopfdruck
darstellen konnten. Dabei gab es eine Änderung der Eingabe: Funktionen sind
zuerst einzugeben, dann erst die Argumente ("sin(30)" statt "30
sin"). Heute gibt es eine neue Generation von Taschenrechnern (TI-92), die
neben der grafischen Darstellung von Funktionen auch die algebraische
Umformungsarbeit unterstützen. Das ist lustiger und erspart mühseliges
Umformen.
Der TI-92 hat neun Bildschirme, die durch APPS 1-9&xnbsp;
aufgerufen werden können:
|
Im HOME-Bildschirm macht man die üblichen Taschenrechneraufgaben, aber
auch die algebraischen Umformungen
|
Der
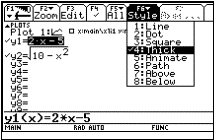
zweite Bildschirm heißt Y=Editor&xnbsp;und dient
zur Eingabe von Funktionen, die im GRAPH-Bildschirm angesehen werden können.
|
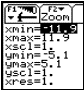
Im WINDOW-Editor&xnbsp;werden die
Intervallgrenzen von x und y eingegeben - oder man wählt einen Standard-ZOOM
aus.
|
|
   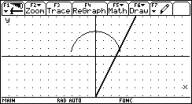
Im GRAPH-Bildschirm können nicht nur Funktionen gezeichnet werden,
man kann sich auch besondere Punkte „tracen“, d.h. deren Koordinaten
können ausgegeben werden. Weiters können die Maxima und Minima ausgegeben
und Tangenten, Text und einiges mehr eingezeichnet werden.
|
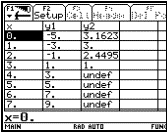
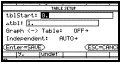
Der TABLE-Bildschirm gibt die Tabelle der Funktionswerte für die eingegebenen
Funktionen aus, nachdem die Startwerte und die Schrittweite im TblSet-Fenster
eingegeben wurden.
|
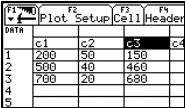
Der DATA/MATRIX-Editor&xnbsp;dient zur
Eingabe von selbsterstellten Tabellen. Ähnlich wie bei einer Tabellenkalkulation
kann man auch rechnen. Spalten können addiert, multipliziert, differenziert,...
werden
(
siehe dazu das Beispiel 14: Mischungsaufgabe).
|
|
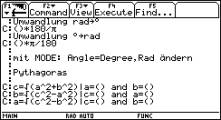 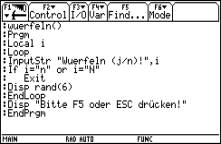 
Der PROGRAM-Editor ermöglicht es, Programme einzugeben. Hier sind
die Erweiterungsmöglichkeiten recht groß, vor allem neue Funktionen
können hier erstellt werden (siehe dazu das Beispiel 17: Geradengleichung
durch 2 Punkte).
|
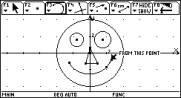
Der GEOMETRIE-Bildschirm liefert eine Konstruktionsmöglichkeit für geometrische
Konstruktionen wie z.B. „Umkreiskonstruktion mittels Streckensymmetralen“.
Auch Animationen und Veränderungen der Figuren sind mit der HAND B &xnbsp;leicht zu
konstruieren
|
Der TEXT-Editor&xnbsp;dient nicht
nur zur Texteingabe, sondern kann auch zur Ausführung von Befehlen dienen.
Eine komplette Kurvendiskussion ist hier speicherbar - ebenso Formeln
und Tips und Tricks. Auch der Inhalt des HOME-Bildschirms ist als Textdatei speicherbar.
|
Die Mathematik kennt natürliche,
ganze, rationale und reelle Zahlen als Grundmengen und die Dezimalzahlen&xnbsp;als Sonderfall der reellen Zahlen. Bei den üblichen Taschenrechnern
tauchen nur die Dezimalzahlen auf, die alle anderen Zahlen annähern
(approximieren). Wie sieht es nun beim TI-92
aus?
Beispiel 2:
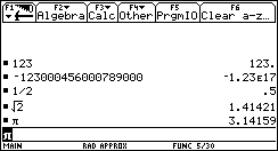
Wie werden im MODE&xnbsp;„EXACT“ die Zahlen 123, -123000456000789000, ½, 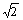 &xnbsp;und p
ausgegeben ?
&xnbsp;und p
ausgegeben ?
 Lösung:
Lösung:
Beispiel 3:
Wie werden im MODE&xnbsp;„APPROXIMATE“ die Zahlen 123,
-123000456000789000, ½, 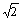 &xnbsp;und p ausgegeben,
wobei „FLOAT6“ und „NORMAL“ als Anzeigeformat ausgewählt wurden?
&xnbsp;und p ausgegeben,
wobei „FLOAT6“ und „NORMAL“ als Anzeigeformat ausgewählt wurden?
Lösung:
Die Tastatur des TI-92 ermöglicht
es, auch Texte&xnbsp;einzugeben. Dazu gibt es auch eine eigene Textverarbeitung&xnbsp;namens „Text Editor“, die man mit APPS&xnbsp; 9&xnbsp; erreicht. Interessant wäre es aber auch, im
HOME-Bildschirm&xnbsp;auszuprobieren, was mit Texten geschieht.
Dabei kann man auch das Einfügen und Löschen&xnbsp;ausprobieren. Auch die Sonderzeichen&xnbsp;sollte man finden können.
Nun werden wir alles löschen&xnbsp;und dann folgende Geheimnachricht schreiben:
Beispiel 6:
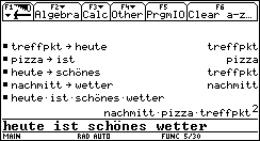
Man schreibe eine
GEHEIMNACHRICHT&xnbsp;(mit Hilfe des Speicherns von Namen auf Variablen), so dass mit
Eingabe von „Heute ist schönes Wetter“ die Nachricht „Treffpunkt Pizza heute
nachmittag“ erscheint.
Lösung:&xnbsp; &xnbsp; Eingabe:
treffpkt STO>
heute&xnbsp;&xnbsp; ENTER
pizza&xnbsp;&xnbsp; STO>
ist&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp; ENTER
heute&xnbsp;&xnbsp; STO> schönes&xnbsp; ENTER
&xnbsp;nachmitt&xnbsp; STO> wetter ENTER
Aufruf:
mit Eingabe des ursprünglichen
Satzes
(eventuell nach dem Löschen&xnbsp;der Eingabe)
Großbuchstaben&xnbsp;bekommt man durch Eingabe mit der
-Taste, die zuerst gedrückt werden
muss.
Löschen&xnbsp;kann man mit der Löschtaste&xnbsp;¬DEL
Umlaute&xnbsp;bekommt man durch:
ö .... 2nd u o
ü .... 2nd u u
ä .... 2nd u a
Einfügen geschieht automatisch, wenn
die Anzeigezeile nicht schwarz ist. Durch Betätigen der Cursortaste (è ) wird die schwarze Anzeige gelöscht und
einfügen ist möglich.
rasche
Cursorbewegungen&xnbsp;erfolgen mit 2nd + CURSOR
alles löschen&xnbsp;erfolgt mit CLEAR in
der Eingabezeile und mit F1 8 <Clear Home>
BEISPIEL 8:&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;
Welchen speziellen
Zahlenwert nimmt der Term&xnbsp;&xnbsp; 7x² -3x +5
für&xnbsp; x = -1&xnbsp;
und&xnbsp; x = 3&xnbsp; an ?
 Lösung:
Lösung:
&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;
BEISPIEL 9:&xnbsp;&xnbsp;&xnbsp;&xnbsp;
Man vereinfache den
Term&xnbsp;&xnbsp; 6x-{[(3x+2y)+2x]-(8x+9y)}
Lösung:
Hier sieht man, dass der TR zwei
Klammerpaare schon bei der Eingabe weglässt, da sie unnötig sind.
BEISPIEL 10:&xnbsp;&xnbsp; Man kürze den
Bruchterm: 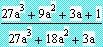
LÖSUNG:
Zur Lösung der Aufgabe
muss man den Zähler und Nenner mit dem Befehl factor faktorisieren und dann den Quotienten bilden:
EINGABE:
&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;
&xnbsp;
BEISPIEL 13: &xnbsp;
Man löse die Gleichung:&xnbsp; (x-3)*(x-2) = (x-5)*(x-6)
LÖSUNG:&xnbsp;
Die
schnelle Methode zur Gleichungslösung ist die Verwendung des Befehls&xnbsp; solve,
den man mit&xnbsp;&xnbsp; F2&xnbsp; 1&xnbsp;
im ALGEBRA-Menü erreicht (oder einfach auf der Tastatur eingibt: