3.12 Realisierung des Alpha-Systems

Es liegt im Wesen der Kryptographie, daß ständig
neue kryptographische Mechanismen erfunden werden und daß sie sich
hinsichtlich sicherer Algorithmen selbst korrigiert. Im folgenden soll
exemplarisch illustriert werden, wie das Alpha-, Beta- und Gamma-System
implementiert werden kann. Hierbei handelt es sich nicht um eine endgültige
und für die langfristige Zukunft gültige Implementierungsvariante,
sondern es werden lediglich Möglichkeiten der Realisierung aufgezeigt.
Die Entscheidung für die eingesetzten Kryptoverfahren kann mithin
zu einem Zeitpunkt in der Zukunft durch Kryptographie-Experten getroffen
werden.
3.12.1 ElGamal-Verschlüsselungsschema
Für das Alpha-System wird das ElGamal-Codierungsschema
(ElGamal, 1985) mit dem Schnorr-Signaturschema verwendet (Schnorr, 1991).
Die Sicherheit des ElGamal Verfahrens ist äquivalent zur Diffie-Hellman-Annahme,
die auf der Komplexität der Berechnung diskreter Logarithmen beruht
(Diffie/Hellman, 1976): Seien p eine Primzahl und g Generator
aus der Menge 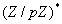 und
(a,b) zwei Zufallszahlen aus
und
(a,b) zwei Zufallszahlen aus 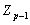 (g
ist
ein Generator mod p, falls es für jedes y von 1 bis
(g
ist
ein Generator mod p, falls es für jedes y von 1 bis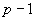 eine
Zahl x gibt mit
eine
Zahl x gibt mit 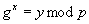 ).
Die Diffie-Hellman-Annahme besagt nun, daß bei gegebenen
).
Die Diffie-Hellman-Annahme besagt nun, daß bei gegebenen 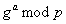 und
und 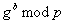 die
Berechnung von
die
Berechnung von 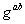 praktisch
undurchführbar ist.
praktisch
undurchführbar ist.
Im weiteren operieren wir in einer Untergruppe 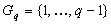 (der
Ordnung
(der
Ordnung 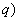 von
von 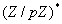 ,
wobei p eine große Primzahl,
,
wobei p eine große Primzahl, 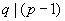 und
und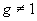 einen
Generator der Ordnung q repräsentiert (Cramer/Gennaro/Schoenmakers,
1997). Diese Darstellungsform wird für das Schnorr-Verfahren benötigt.
einen
Generator der Ordnung q repräsentiert (Cramer/Gennaro/Schoenmakers,
1997). Diese Darstellungsform wird für das Schnorr-Verfahren benötigt.
Schlüsselerzeugungs-Algorithmus 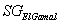
-
Wähle eine zufällige Primzahl
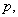
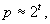 Der
Wert
Der
Wert 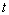 muß
als Sicherheitsparameter entsprechend gewählt werden.
muß
als Sicherheitsparameter entsprechend gewählt werden.
-
Wähle einen Generator
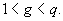
-
Erzeuge einen zufälligen geheimen Schlüssel
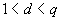 sowie
einen öffentlichen Schlüssel
sowie
einen öffentlichen Schlüssel 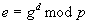 .
.
-
Ausgabeparameter:
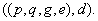
Verschlüsselungs-Algorithmus 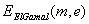
-
Wähle eine Zufallszahl
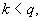
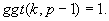
-
Ausgabeparameter:
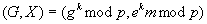
Entschlüsselungs-Algorithmus 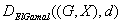
-
Ausgabeparameter:
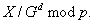
Die Systemparameter bestehen aus dem öffentlichen Schlüssel 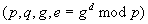 und
korrespondierendem geheimen Schlüssel d aus
und
korrespondierendem geheimen Schlüssel d aus 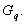 Um
den nötigen Speicherplatz pro Schlüsselpaar zu reduzieren, können
alle Teilnehmer und Instanzen, die mit einer LA korrespondieren,
gemeinsam die eindeutigen Systemparameter (p,q,g) verwenden. Diese
Werte werden dann für die weitere Generierung neuer Schlüssel
als konstant vorausgesetzt.
Um
den nötigen Speicherplatz pro Schlüsselpaar zu reduzieren, können
alle Teilnehmer und Instanzen, die mit einer LA korrespondieren,
gemeinsam die eindeutigen Systemparameter (p,q,g) verwenden. Diese
Werte werden dann für die weitere Generierung neuer Schlüssel
als konstant vorausgesetzt.
Die Entschlüsselung ist korrekt, da 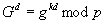 und
somit folgt
und
somit folgt
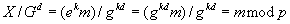 .
.
3.12.2 Schnorr-Signaturschema
Die Systemparameter sind dieselben wie im ElGamal-Schema.
Das Schnorr-Signaturschema (Schnorr, 1991) verwendet zusätzlich eine
kryptographisch sichere Hash-Funktion.
Schlüsselerzeugungs-Algorithmus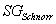
-
Analog wie ElGamal (Cramer/Gennaro/Schoenmakers, 1997).
Signatur-Algorithmus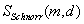
-
Wähle einen geheimen Zufallsschlüssel
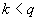 und
berechne
und
berechne
-
den korrespondierenden öffentlichen Schlüssel
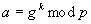 .
.
-
Berechne
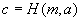 .
.
-
Berechne
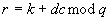 .
.
-
Ausgabeparameter
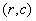
Verifikations-Algorithmus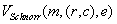
-
Überprüfe
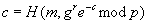
3.12.3 Kollektivschlüssel-Erzeugungsprotokoll
Wir realisieren das oben beschriebene Kollektivschlüssel-Erzeugungsprotokoll
im Schnorr-ElGamal-System. Das Kollektivschlüssel-Erzeugungsprotokoll
stellt den Spezialfall n=k des (n,k)-Schwellenwertschemas
zur Schlüsselverteilung von Pedersen dar (Pedersen, 1991).
-
Jeder Protokollteilnehmer wählt einen geheimen Zufallsschlüssel
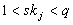 und
berechnet den korrespondierenden öffentlichen Schlüssel
und
berechnet den korrespondierenden öffentlichen Schlüssel 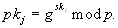
-
Jeder Teilnehmer veröffentlicht seinen Teilschlüssel
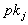 und
erbringt einen Nachweis, daß es sich tatsächlich um einen korrekten
öffentlichen Schlüssel handelt. Der Teilnehmer signiert deshalb
seinen öffentlichen Schlüssel, erhält
und
erbringt einen Nachweis, daß es sich tatsächlich um einen korrekten
öffentlichen Schlüssel handelt. Der Teilnehmer signiert deshalb
seinen öffentlichen Schlüssel, erhält 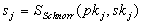 und
überträgt insgesamt
und
überträgt insgesamt 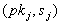 an
alle Teilnehmer.
an
alle Teilnehmer.
-
Jeder Teilnehmer kann überprüfen, ob die öffentlichen
Schlüssel korrekt sind, indem er die publizierten Signaturen verifiziert,
d.h.
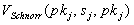 für
für 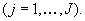
-
Dann berechnet ein Teilnehmer den öffentlichen Kollektivschlüssel
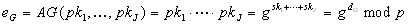 ,der
im X.500 publiziert wird.
,der
im X.500 publiziert wird.
3.12.4 Kollektives
Entschlüsselungsprotokoll
Wir realisieren das oben beschriebene Kollektivschlüssel-Erzeugungsprotokoll
im Schnorr-ElGamal-System. Das Protokoll zur Entschlüsselung wird
für ein codiertes Datum 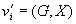 dargestellt.
Wenn der Wahlschein gemischt codiert wurde, dann ist
dargestellt.
Wenn der Wahlschein gemischt codiert wurde, dann ist 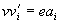 (siehe
3.8.8). Ansonsten gilt
(siehe
3.8.8). Ansonsten gilt 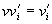 .
.
-
Jede Einheit j des Dechiffrierungskreises berechnet
mit ihrem geheimen Zufallsschlüssel
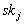 eine
Teilentschlüsselung
eine
Teilentschlüsselung 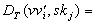
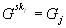
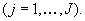
-
Jeder Teilnehmer veröffentlicht
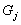 und
erbringt einen Nachweis, daß es sich tatsächlich um eine korrekte
Entschlüsselung handelt. Der Teilnehmer zeigt durch einen Beweis,
daß
und
erbringt einen Nachweis, daß es sich tatsächlich um eine korrekte
Entschlüsselung handelt. Der Teilnehmer zeigt durch einen Beweis,
daß 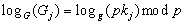 gilt,
ohne dabei seinen geheimen Schlüssel
gilt,
ohne dabei seinen geheimen Schlüssel 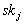 zu
enthüllen. Den Beweis realisiert z.B. eine nichtinteraktive modifizierte
Variante der Schnorr-Signaturprotokolls von Chaum und Pedersen (Chaum/Pedersen,
1993), das wir als Chaum-Schnorr-Pedersen-Signaturschema bezeichnen. Mit
diesem Protokoll kann die korrekte Potenzierung von
zu
enthüllen. Den Beweis realisiert z.B. eine nichtinteraktive modifizierte
Variante der Schnorr-Signaturprotokolls von Chaum und Pedersen (Chaum/Pedersen,
1993), das wir als Chaum-Schnorr-Pedersen-Signaturschema bezeichnen. Mit
diesem Protokoll kann die korrekte Potenzierung von 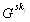 überprüft
werden. Der Server berechnet die Signatur
überprüft
werden. Der Server berechnet die Signatur 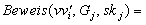
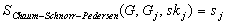 und
überträgt insgesamt
und
überträgt insgesamt 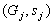 an
alle Teilnehmer. Der Chaum-Schnorr-Pedersen-Algorithmus wird am Ende dieses
Abschnittes präsentiert. Falls ein Teilnehmer des Dechiffrierungskreises
diesen Beweis verweigert, dann gilt dieser als schuldig. Damit das Protokoll
erheblich beschleunigt wird, können und sollen sowohl die Teilentschlüsselungen
als auch die Beweisführung von jedem Protokollteilnehmer vor der Wahlzeit
parallel vorausberechnet und erst nach Ende der Wahlzeit publiziert werden.
Nach dem Ende der Wahl-zeit übertragen die Einheiten des Dechiffrierungskreises
gleichzeitig sämtliche Teildecodierungen an alle Teilnehmer (per Multicast).
an
alle Teilnehmer. Der Chaum-Schnorr-Pedersen-Algorithmus wird am Ende dieses
Abschnittes präsentiert. Falls ein Teilnehmer des Dechiffrierungskreises
diesen Beweis verweigert, dann gilt dieser als schuldig. Damit das Protokoll
erheblich beschleunigt wird, können und sollen sowohl die Teilentschlüsselungen
als auch die Beweisführung von jedem Protokollteilnehmer vor der Wahlzeit
parallel vorausberechnet und erst nach Ende der Wahlzeit publiziert werden.
Nach dem Ende der Wahl-zeit übertragen die Einheiten des Dechiffrierungskreises
gleichzeitig sämtliche Teildecodierungen an alle Teilnehmer (per Multicast).
-
Jeder Teilnehmer kann überprüfen, ob die öffentlichen
Schlüssel korrekt sind, indem dieser die publizierten Signaturen verifiziert,
d.h. er verifiziert
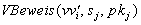 =
= 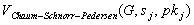 für
für 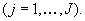 Zur
Erreichung erhöhter Auswertungsgeschwindigkeit sollte VBeweis erst
nach dem Ende der Resultate durchgeführt werden.
Zur
Erreichung erhöhter Auswertungsgeschwindigkeit sollte VBeweis erst
nach dem Ende der Resultate durchgeführt werden.
-
Dann können alle Protokollteilnehmer die gemeinsame
Potenzierung
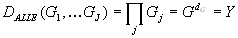
vornehmen und daraus das entschlüsselte Datum 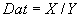 berechnen.
berechnen.
Erfolgte eine hybride Codierung dann gilt 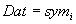 ,
sonst
,
sonst 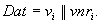
3.12.4.1 Chaum-Schnorr-Pedersen-Signaturschema
Die Systemparameter sind dieselben wie im ElGamal-Schema.
Schlüsselerzeugungs-Algorithmus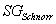
Signatur-Algorithmus
-
Wähle einen geheimen Zufallsschlüssel
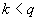 und
berechne die korrespondierenden öffentlichen Werte
und
berechne die korrespondierenden öffentlichen Werte 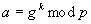 und
und 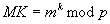 .
.
-
Berechne
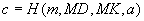 .
.
-
Berechne
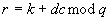 .
.
-
Ausgabeparameter
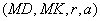
Verifikations-Algorithmus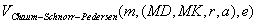
-
Berechne
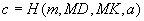 .
.
-
Überprüfe
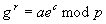 .
.
-
Überprüfe
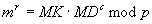
3.12.5 Symmetrisches
Codierungsschema
Wir treffen hier keine besondere Auswahl des benützten
symmetrischen Codierungsschemas. Mögliche Realisierungsarten sind
u.a. DES, IDEA und BLOWFISH (siehe Schneier, 1996).
3.12.6 Hash-Funktion
und Commitment
Als sichere Hash-Funktion verwenden wir den Secure Hash
Algorithm (SHA). SHA produziert für jede Eingabe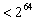 Bit
eine Ausgabe der Länge 160 Bit, die als Message-Digest bezeichnet
wird. "SHA wird als sicher bezeichnet, da er so entworfen wurde, daß
es vom Berechnungsaufwand her nicht durchführbar ist, eine Nachricht
zu einem vorgegebenen Message Digest zu bestimmen oder zwei Nachrichten
zu finden, die den gleichen Message Digest ergeben" (Schneier, 1996,
S. 504). Zur Zeit existieren keine bekannten Angriffe gegen SHA. Zudem
bietet SHA einen akzeptablen Schutz vor Brute-Force-Angriffe (einschließlich
dem Geburtstagsangriff).
Bit
eine Ausgabe der Länge 160 Bit, die als Message-Digest bezeichnet
wird. "SHA wird als sicher bezeichnet, da er so entworfen wurde, daß
es vom Berechnungsaufwand her nicht durchführbar ist, eine Nachricht
zu einem vorgegebenen Message Digest zu bestimmen oder zwei Nachrichten
zu finden, die den gleichen Message Digest ergeben" (Schneier, 1996,
S. 504). Zur Zeit existieren keine bekannten Angriffe gegen SHA. Zudem
bietet SHA einen akzeptablen Schutz vor Brute-Force-Angriffe (einschließlich
dem Geburtstagsangriff).
Die Commitment-Funktion (BC) kann durch unterschiedliche
Verfahren (u.a. mit symmetrischer Kryptographie oder mit sicheren Hash-Funktionen
realisiert werden) (Realisierung siehe: Schneier, 1996, S. 104-107).





![]() und
(a,b) zwei Zufallszahlen aus
und
(a,b) zwei Zufallszahlen aus ![]() (g
ist
ein Generator mod p, falls es für jedes y von 1 bis
(g
ist
ein Generator mod p, falls es für jedes y von 1 bis![]() eine
Zahl x gibt mit
eine
Zahl x gibt mit ![]() ).
Die Diffie-Hellman-Annahme besagt nun, daß bei gegebenen
).
Die Diffie-Hellman-Annahme besagt nun, daß bei gegebenen ![]() und
und ![]() die
Berechnung von
die
Berechnung von ![]() praktisch
undurchführbar ist.
praktisch
undurchführbar ist.
![]() (der
Ordnung
(der
Ordnung ![]() von
von ![]() ,
wobei p eine große Primzahl,
,
wobei p eine große Primzahl, ![]() und
und![]() einen
Generator der Ordnung q repräsentiert (Cramer/Gennaro/Schoenmakers,
1997). Diese Darstellungsform wird für das Schnorr-Verfahren benötigt.
einen
Generator der Ordnung q repräsentiert (Cramer/Gennaro/Schoenmakers,
1997). Diese Darstellungsform wird für das Schnorr-Verfahren benötigt.
![]()
![]() und
somit folgt
und
somit folgt
![]() .
.![]()
![]()
![]() dargestellt.
Wenn der Wahlschein gemischt codiert wurde, dann ist
dargestellt.
Wenn der Wahlschein gemischt codiert wurde, dann ist ![]() (siehe
3.8.8). Ansonsten gilt
(siehe
3.8.8). Ansonsten gilt ![]() .
.
![]()
![]() Bit
eine Ausgabe der Länge 160 Bit, die als Message-Digest bezeichnet
wird. "SHA wird als sicher bezeichnet, da er so entworfen wurde, daß
es vom Berechnungsaufwand her nicht durchführbar ist, eine Nachricht
zu einem vorgegebenen Message Digest zu bestimmen oder zwei Nachrichten
zu finden, die den gleichen Message Digest ergeben" (Schneier, 1996,
S. 504). Zur Zeit existieren keine bekannten Angriffe gegen SHA. Zudem
bietet SHA einen akzeptablen Schutz vor Brute-Force-Angriffe (einschließlich
dem Geburtstagsangriff).
Bit
eine Ausgabe der Länge 160 Bit, die als Message-Digest bezeichnet
wird. "SHA wird als sicher bezeichnet, da er so entworfen wurde, daß
es vom Berechnungsaufwand her nicht durchführbar ist, eine Nachricht
zu einem vorgegebenen Message Digest zu bestimmen oder zwei Nachrichten
zu finden, die den gleichen Message Digest ergeben" (Schneier, 1996,
S. 504). Zur Zeit existieren keine bekannten Angriffe gegen SHA. Zudem
bietet SHA einen akzeptablen Schutz vor Brute-Force-Angriffe (einschließlich
dem Geburtstagsangriff).