3.13
Realisierung des Beta-Systems

Für das Beta-System verwenden wir das blinde Schnorr-Signaturschema
(Stadler, 1996, S. 35).
3.13.1 Blindes
Schnorr-Signaturprotokoll
Die Parameter entsprechen dem Schnorr-Signaturschema.
Schlüsselerzeugungs-Algorithmus 
-
Wähle einen zufälligen Schlüssel
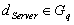 und
berechne
und
berechne 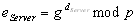 und
liefere als Ausgabeparameter das Paar
und
liefere als Ausgabeparameter das Paar 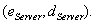
Blinde Signatur-Algorithmus 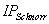

Zunächst erzeugt Server einen zufälligen geheimen
Schlüssel 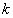 aus
aus 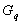 und
berechnet den zugehörigen öffentlichen Zufallsschlüssel
und
berechnet den zugehörigen öffentlichen Zufallsschlüssel
-
Der Client verdeckt a, indem er zwei zufällige
Transformationsschlüssel
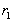 und
und  aus
aus  auswählt
und
auswählt
und
berechnet,
woraus Client die blinden Wert  gewinnt.
gewinnt.
-
Der Client berechnet seine Signatur
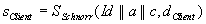 und
sendet das authentifizierte Datenpaket
und
sendet das authentifizierte Datenpaket  zum
Server.
zum
Server.
-
Der Server führt Wahlbedingungen(
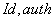 )
aus und antwortet daraufhin mit dem
)
aus und antwortet daraufhin mit dem 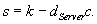
-
Client überprüft nun ob,
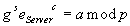 gilt.
gilt.
-
Anschließend transformiert Client

-
Nach Ablauf des Protokolls liefert Client
 wobei
wobei  ist.
ist.
Verifikations-Algorithmus 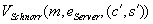
-
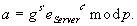
-
Falls
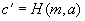 ist, dann liefert die Ausgabe GÜLTIG, sonst UNGÜLTIG.
ist, dann liefert die Ausgabe GÜLTIG, sonst UNGÜLTIG.
Außerdem publiziert der Server für jeden Teilnehmer
den Nachweis 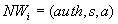 mit
seiner Signatur im BBS. Dadurch existiert ein öffentlicher
Nachweis, daß der Server tatsächlich eine blinde Signatur leistete.
mit
seiner Signatur im BBS. Dadurch existiert ein öffentlicher
Nachweis, daß der Server tatsächlich eine blinde Signatur leistete.
Als Alternative zum blinden Schnorr-Signaturschema wäre
beispielsweise eine blinde RSA-Variante durchführbar.
3.13.2 RSA-Verschlüsselungsschema
Das populärste asymmetrische Codierungsverfahren
RSA wurde von Ron Rivest, Adi Shamir und Leonard Adleman 1978 publiziert
(Rivest/Shamir/Adleman, 1978) und hielt jahrelanger Kryptoanalyse stand.
Die Systemparameter bestehen aus dem öffentlichen
Schlüssel 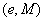 und
dem geheimen Schlüssel
und
dem geheimen Schlüssel  Jeder
Inhaber eines geheimen Schlüssels benötigt einen eindeutigen
Modulus
Jeder
Inhaber eines geheimen Schlüssels benötigt einen eindeutigen
Modulus 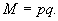 Außerdem
müssen die beiden Primzahlen p und q geheim bleiben.
Das RSA Verschlüsselungsschema besteht aus drei Algorithmen:
Außerdem
müssen die beiden Primzahlen p und q geheim bleiben.
Das RSA Verschlüsselungsschema besteht aus drei Algorithmen:
Schlüsselerzeugungs-Algorithmus 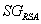
-
Wähle zwei zufällige und gleichlange Primzahlen
p
und
q,
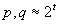 .
Der Wert t dient als Sicherheitsparameter.
.
Der Wert t dient als Sicherheitsparameter.
-
Berechne die Eulersche Phi-Funktion
 und
Modulus
und
Modulus 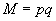 .
.
-
Wähle einen Codierungsschlüssel e, der zu
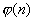 relativ
prim ist, d.h. es gilt
relativ
prim ist, d.h. es gilt 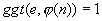 .
.
-
Berechne

-
Ausgabeparameter: Schlüsselpaar
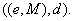
Verschlüsselungs-Algorithmus
-
Ausgabeparameter:

Entschlüsselungs-Algorithmus 
-
Ausgabeparameter:
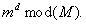
Die Sicherheitsannahme des RSA-Systems beruht darauf, daß
die Wiederherstellung des Klartextes bei gegebenem öffentlichen Schlüssel
und Chiffretext der Faktorisierung des Produkts beider Primzahlen (p,q)
entspricht (Faktorisierungsproblem). Seit Jahrhunderten versuchten Mathematiker
erfolglos, Algorithmen zur schnellen Primfaktorzerlegung zu finden. Ein
Brute-Force-Angriff, der jeden möglichen geheimen Schlüssel ausprobiert,
gilt als ineffizienter als der Versuch, M zu faktorisieren (Schneier,
1996).
3.13.3 RSA-Signaturschema
Das RSA-Signaturschema hat die gleichen Parameter wie
das RSA-Codierungsschema.
Schlüsselerzeugungs-Algorithmus
Siehe RSA-Verschlüsselungschema.
Signatur-Algorithmus
-
Berechne

-
Ausgabeparameter: Signatur s.
Verifikations-Algorithmus 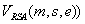
-
Berechne die Hash-Summe
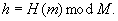
-
Berechne
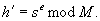
-
Falls
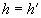
dann liefere den Ausgabewert GÜLTIG, sonst UNGÜLTIG.
3.13.4 Blindes
RSA-Signaturschema
Das blinde RSA-Signaturschema basiert auf den Parametern
des RSA-Kryptosystems. Die erste RSA-Implementierung stammt von David Chaum
(Chaum, 1985). Eine RSA-Variante wird auch für E-Cash eingesetzt.
Schlüsselerzeugungs-Algorithmus
Der Schlüsselerzeugungs-Algorithmus ist analog zum
RSA-Codierungsschema. Der Algorithmus liefert als Ausgabeparameter das
Paar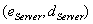
Blinde Signatur-Algorithmus 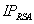

-
Client erzeugt einen zufälligen Transformationsschlüssel
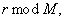 camoufliert
m
und erhält
camoufliert
m
und erhält 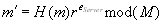 .
Dann signiert er
.
Dann signiert er 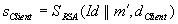 und
sendet
und
sendet 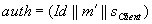 zum
Server.
zum
Server.
-
Der Server überprüft Wahlbedingungen(
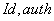 )unterzeichnet
)unterzeichnet 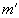 mit
seinem Signaturschlüssel
mit
seinem Signaturschlüssel  ,
und sendet das Resultat
,
und sendet das Resultat  zum
Client zurück.
zum
Client zurück.
-
Der Client entfernt den Transformationsschlüssel
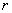 durch
Anwendung der Rücktransformation
durch
Anwendung der Rücktransformation  und
erlangt eine gültige Signatur
und
erlangt eine gültige Signatur 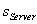 zu m.
zu m.
Verifikations-Algorithmus
Dieser funktioniert analog zum RSA-Signaturverifikations-Algorithmus.
Außerdem publiziert der Server für jeden Teilnehmer
den Nachweis 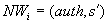 mit
seiner Signatur im BBS.
mit
seiner Signatur im BBS.
3.13.5 Erweiterter
blinder Schnorr-Signatur-Algorithmus
In diesem Abschnitt definieren wir eine Implementierung
des erweiterten Schnorr-Signatur-Algorithmus, um das parallele Ausstellen
von Zertifikaten zu erreichen. Dieser Algorithmus wurde bisher noch nicht
publiziert.
Erweiterter blinder Schnorr-Signatur-Algorithmus
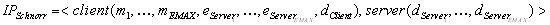
-
Der Server erzeugt EMAX zufällige geheime Schlüssel
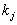 aus
aus 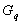 und
berechnet die öffentlichen Zufallsschlüssel
und
berechnet die öffentlichen Zufallsschlüssel

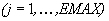
und
sendet 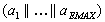 zum
Client.
zum
Client.
-
Der Client verdeckt
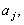 indem
er zwei zufällige Transformationsschlüssel
indem
er zwei zufällige Transformationsschlüssel  und
und 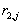 aus
aus 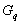 auswählt
und
auswählt
und 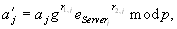
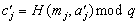
berechnet,
woraus Client die blinden Werte 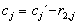 gewinnt
gewinnt 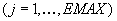 .
.





![]()
aus
und berechnet den zugehörigen öffentlichen Zufallsschlüssel
![]() und
dem geheimen Schlüssel
und
dem geheimen Schlüssel ![]() Jeder
Inhaber eines geheimen Schlüssels benötigt einen eindeutigen
Modulus
Jeder
Inhaber eines geheimen Schlüssels benötigt einen eindeutigen
Modulus ![]() Außerdem
müssen die beiden Primzahlen p und q geheim bleiben.
Das RSA Verschlüsselungsschema besteht aus drei Algorithmen:
Außerdem
müssen die beiden Primzahlen p und q geheim bleiben.
Das RSA Verschlüsselungsschema besteht aus drei Algorithmen:
![]()
![]()
![]()
![]()
![]()
![]()
![]() mit
seiner Signatur im BBS.
mit
seiner Signatur im BBS.
![]()
![]() zum
Server.
zum
Server.