Kegelschnitte

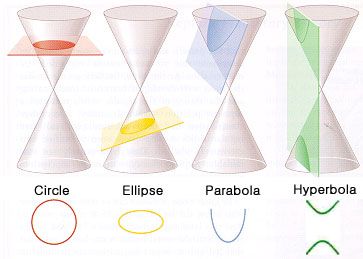
Schneidet man einen Kegel mit einer Ebene, so erhält man - je nachdem, wie stark die Ebene geneigt ist - einen Kreis, eine Ellipse, eine Parabel oder eine Hyperbel.

 

Die Ellipse

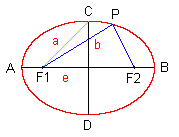Die Ellipse besteht aus allen Punkten, für die die Summe der Abstände von zwei festen Punkten - den Brennpunkten - konstant ist.
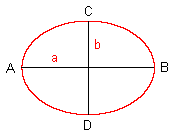A, B: Hauptscheitel
C, D: Nebenscheitel
F1, F2: Brennpunkte
2a: Hauptachse
2b: Nebenachse
e: Brennweite (lineare Exzentrizität)

1. Hauptlage: Mittelpunkt im Koordinatenursprung, Hauptachse auf der x-Achse
2. Hauptlage: Mittelpunkt im Koordinatenursprung, Hauptachse auf der y-Achse

Definition:

ell = {X / XF1 + XF2 = 2a}

Brennweite:

e² = a² - b²

Gleichung in 1. Hauptlage:

Gleichung in 2. Hauptlage:

 

Die Hyperbel

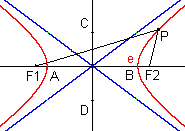Die Hyperbel besteht aus allen Punkten, für die die Differenz der Abstände von den Brennpunkten konstant ist. Sie besteht aus zwei Ästen und besitzt zwei Asymptoten.
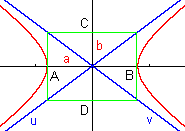A, B: Hauptscheitel
C, D: Nebenscheitel
F1, F2: Brennpunkte
2a: Hauptachse
2b: Nebenachse
e: Brennweite (lineare Exzentrizität)
u, v: Asymptoten

Bei einer gleichseitigen Hyperbel ist a = b.
1. und 2. Hauptlage definiert man wie bei der Ellipse.

Definition:

hyp = {X / |XF1 - XF2| = 2a}

Brennweite:

e² = a² + b²

Gleichung in 1. Hauptlage:

Gleichung in 2. Hauptlage:

Gleichung der Asymptoten
(1. Hauptlage):

 

Die Parabel

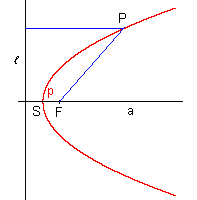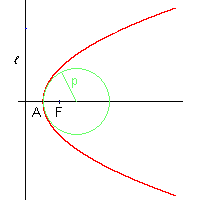
Die Parabel hat nur einen Brennpunkt. Sie besteht aus allen Punkten, die vom Brennpunkt denselben Abstand wie von der Leitlinie haben.

S: Scheitel
F: Brennpunkt
l: Leitlinie
a: Achse
p: Parameter (Abstand Brennpunkt - Leitlinie)
e: Brennweite (Abstand Brennpunkt - Scheitel)

1. Hauptlage: Scheitel im Koordinatenursprung, Achse auf der positiven x-Achse
2. Hauptlage: Scheitel im Koordinatenursprung, Achse auf der positiven y-Achse

Definition:

par = {X / XF = Xl}

Brennweite:

p = 2e

Gleichung in 1. Hauptlage:

y² = 2px

Gleichung in 2. Hauptlage:

x² = 2py

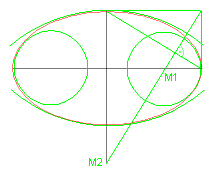
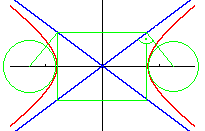
Eine Hilfe beim Zeichnen eines Kegelschnitts sind die Scheitelschmiegkreise:

Lernziele:

  • Ich kann die Gleichung einer Ellipse oder Hyperbel bestimmen, wenn die Achsen gegeben sind.
  • Ich kann die Gleichung einer Ellipse oder Hyperbel bestimmen, wenn eine Achse und e bzw. ein Punkt gegeben sind.
  • Ich kann aus der Gleichung einer Ellipse oder Hyperbel die Achsen ablesen.
  • Ich kann die Gleichung einer Parabel bestimmen, wenn p gegeben ist.
  • Ich kann die Gleichung einer Parabel bestimmen, wenn ein Punkt gegeben ist.
  • Ich kann aus der Gleichung eines Kegelschnitts die Koordinaten der Brennpunkte bestimmen.
  • Ich kann entscheiden, ob ein Punkt auf einem Kegelschnitt liegt.
  • Ich kann die Schnittpunkte eines Kegelschnitts und einer Geraden berechnen.
  • Ich kann die Schnittpunkte zweier Kegelschnitte berechnen.

(Alle Kegelschnitte in Hauptlage)

Übungen

Für besonders Interessierte: Mehr über Kegelschnitte

Zum Inhaltsverzeichnis