Kegelschnitte

Inhalt

1. Einleitung

1.1. Kegelschnitte im Alltag

Die einfachsten geometrischen Kurven sind die Gerade und der Kreis. Doch in unserer Umgebung stoßen wir auf eine Fülle anderer Kurven, zum Beispiel:

Wenn wir eine Salami schräg anschneiden, hat die Schnittfläche die Form einer Ellipse.	Ein Ball, der schräg nach oben geworfen wird, beschreibt eine Parabel.	An einem Bleistift sehen wir Kurven zwischen der Spitze und den Seitenflächen. Eine solche Kurve heißt Hyperbel.

Und last not least sind die Bahnen der Himmelskörper um die Sonne - je nach Geschwindigkeit - Ellipsen, Parabeln oder Hyperbeln.

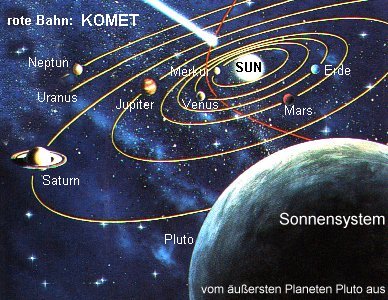
Schon die alten Griechen wußten, dass man alle diese Kurven erhalten kann, wenn man einen Kegel mit einer Ebene schneidet - daher bezeichnet man sie als "Kegelschnitte".

Im Schulunterricht werden die Kegelschnitte meist mit Hilfe der Brennpunktsdefinition eingeführt. Ich möchte in diesem Artikel, nach einem eher intuitiven Einstieg, die wichtigsten Stationen der historischen Entwicklung nachzeichnen, die bis zur heute üblichen Behandlung in der analytischen Geometrie geführt hat.

1.2. Eigenschaften (erster Überblick)

Wir betrachten einen Drehkegel, dessen Mantellinien mit der Achse den Winkel φ einschließen. Dieser Kegel wird von einer Ebene geschnitten. Den Winkel zwischen der Kegelachse und der Ebene bezeichnen wir mit ω.

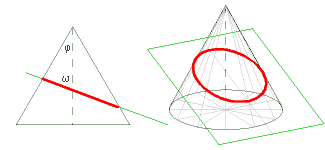	Ist ω > φ, ist die Schnittkurve eine Ellipse. (Steht die Ebene normal auf die Achse, d.h. ω = 90°, ergibt sich ein Kreis.)
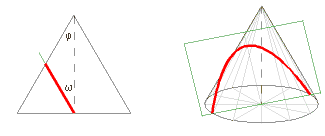	Ist ω = φ (die Ebene ist also parallel zu einer Mantellinie des Kegels), erhalten wir eine Parabel.
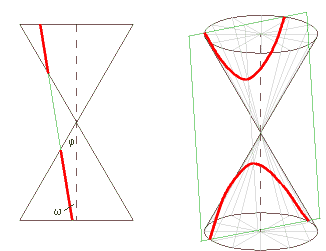	Im Fall ω < φ müssen wir den Kegel zu einem Doppelkegel ergänzen. Die Schnittkurve, eine Hyperbel, besteht aus zwei Teilen.

(Wenn die Schnittebene durch die Spitze des Kegels geht, erhalten wir als Schnittfigur einen Punkt, eine Gerade oder ein Geradenpaar. Das bezeichnet man als "ausgearteten" Kegelschnitt.)

Wir wollen zuerst einmal die verschiedenen Kegelschnitte betrachten und einige Eigenschaften und Bezeichnungen zusammenstellen. Die Beweise folgen später.

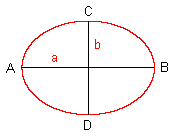	Die Ellipse (man kann sie auch als zusammengedrückten Kreis beschreiben) hat zwei Symmetrieachsen. Die längere Achse bezeichnet man als Hauptachse mit der Länge 2a, ihre Schnittpunkte mit der Ellipse sind die Hauptscheitel A und B. Die kürzere Achse ist die Nebenachse 2b, sie schneidet die Ellipse in den Nebenscheiteln C und D. Ist a = b, wird aus der Ellipse ein Kreis.
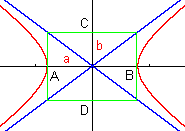	Die Hyperbel hat ebenfalls zwei Symmetrieachsen, von denen aber nur eine - die Hauptachse - die Kurve schneidet. Ihre Länge beträgt wieder 2a, die Schnittpunkte sind die Hauptscheitel A und B. Außerdem gibt es zwei Geraden, denen sich die Kurve immer mehr annähert - die Asymptoten der Hyperbel. Wir können nun ein Rechteck zeichnen, das durch A und B geht und dessen Eckpunkte auf den Asymptoten liegen. Die Höhe dieses Asymptotenrechtecks gibt uns die Länge 2b der Nebenachse an, die Schnittpunkte mit der zweiten Symmetrieachse bezeichnet man als Nebenscheitel C und D. Das sind allerdings keine Hyperbelpunkte. Eine Hyperbel, bei der a = b ist, heißt gleichseitige Hyperbel. Ihre Asymptoten stehen normal aufeinander.
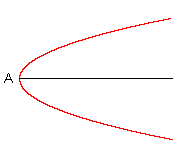	Die Parabel hat nur eine Achse und einen Scheitel A (oft auch mit S bezeichnet).

1.3. Kurzer historischer Überblick

Als Entdecker der Kegelschnitte gilt Menaichmos (ca. 350 v.Chr.). Er stieß auf diese Kurven, als er versuchte, das Problem der Würfelverdopplung zu lösen.

Euklid (ca. 300 v.Chr.) schrieb ein Buch über Kegelschnitte, das leider verlorengegangen ist.

Archimedes (287 - 212 v.Chr.) berechnete den Flächeninhalt der Ellipse und des Parabelabschnitts. Er untersuchte auch Ellipsoide, Paraboloide und Hyperboloide - Körper, die entstehen, wenn ein Kegelschnitt um seine Achse rotiert. Es gelang ihm, das Volumen der Segmente zu berechnen, die beim Schnitt eines solchen Rotationskörpers mit einer beliebigen Ebene entstehen. Die Methoden, die er dabei verwendete, kann man als Vorläufer der Integralrechnung betrachten.

Ursprünglich betrachtete man in der griechischen Mathematik nur den Fall, dass die Schnittebene auf eine Mantellinie des Kegels normal steht. Dementsprechend sprach man vom "Schnitt am rechtwinkligen, spitzwinkligen oder stumpfwinkligen Kegel". Den Parameter des Kegelschnitts nannte man "das Stück (vom Scheitel) bis zur (Kegel-)Achse".

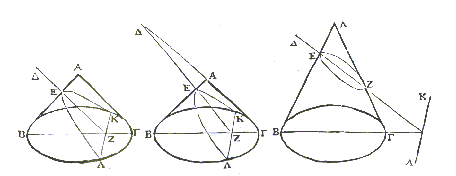
Apollonius von Perge (ca. 260 - 190 v.Chr.) zeigte, dass man alle drei Arten von Kegelschnitten durch verschiedene Schnitte an einem einzigen Kegel erhalten kann. Er schrieb die "Konika", das bedeutendste Werk der Antike über dieses Thema. Darin führte er auch die Bezeichnungen Ellipse, Parabel und Hyperbel ein. (Das Bild ist eine Illustration zu einer "Konika"-Ausgabe aus dem 18 Jahrhundert.)

Auch in der Neuzeit wurden die Kegelschnitte immer wieder untersucht. René Descartes (1596 - 1650) schuf mit der Analytischen Geometrie die Voraussetzungen dafür, dass wir die Eigenschaften der Kegelschnitte anhand ihrer Gleichungen untersuchen können. Er entdeckte auch eine Methode zur Winkeldreiteilung mithilfe einer festen Parabel.

Johannes Kepler (1571 - 1630) beschäftigte sich mit Kegelschnitten zuerst im Zusammenhang mit optischen Linsen, bevor er sein erstes Bewegungsgesetz entdeckte:

Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.

Blaise Pascal (1623 - 1662) schrieb mit 16 Jahren eine Abhandlung über Kegelschnitte, die leider verschollen ist, und wenig später seinen "Essay pour les coniques". Der nach ihm benannte Satz über Sechsecke in einem Kegelschnitt ("hexagramme mystique") wurde wichtig für die Entwicklung der projektiven Geometrie.

Weiter: Die "klassische" Definition