Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Der griechische Mathematiker Pappos von Alexandria (ca. 290 - 350) untersuchte folgendes Problem: Gegeben sind vier Geraden a, b, c und d. Was ist die Menge (oder: der geometrische Ort) aller Punkte, für die das Verhältnis
konstant ist?
(Wenn zwei der Geraden zusammenfallen, erhält man als Spezialfall das Problem des Orts zu drei Geraden.)
Schon in der Antike war bekannt, dass diese Menge ein Kegelschnitt ist. Angeblich hat das schon Apollonius bewiesen; man weiß aber nicht genau, wie sein Beweis lautete.
Dieses Problem hat wesentlich zur Entwicklung der analytischen Geometrie beigetragen. René Descartes demonstrierte die Überlegenheit seiner "analytischen Methode", indem er das Problem löste und sogar auf mehr als vier Geraden verallgemeinerte (dabei ergeben sich algebraische Kurven höheren Grades).
Analytischer Beweis:
Der Originalbeweis von Descartes liest sich für uns etwas mühsam, weil er noch keine rechtwinkeligen Koordinaten benutzt. In moderner Form kann man ihn ungefähr so schreiben:
Den Abstand des Punktes P(x/y) von der Geraden g: ax + by = c kann man mithilfe der Hesse'schen Normalform berechnen:
oder einfacher: Pg = αx + βy - γ
Die gesuchte Kurve hat daher die Gleichung
(α1x + β1y - γ1) (α3x + β3y - γ3) = k(α2x + β2y - γ2) (α4x + β4y - γ4)
Wenn man das ausmultipliziert, erhält man eine quadratische Gleichung in zwei Variablen. Wie wir wissen (und wie schon zur Zeit von Descartes bekannt war), ist das die Gleichung eines Kegelschnitts in allgemeiner Lage.
Geometrischer Beweis:
Ich werde beweisen: Wenn ein Kegelschnitt durch die vier Schnittpunkte A, B, C, D der Geraden a, b, c und d geht, ist für alle seine Punkte das Verhältnis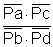 konstant. (Das ist die Umkehrung der obigen Aussage.)
konstant. (Das ist die Umkehrung der obigen Aussage.)
Zuerst betrachten wir den Spezialfall, dass es sich um einen Kreis handelt. Wir werden zeigen, dass in diesem Fall das Verhältnis 1 ist:
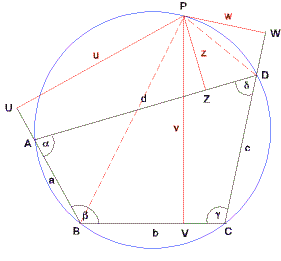
Sei ABCD ein Sehnenviereck, P ein beliebiger Punkt auf dem Umkreis, u = Pa, v = Pb, w = Pc und z = Pd die Normalabstände von P zu den Seiten und U, V, W und Z die Fußpunkte der Normalen. Wegen des Peripheriewinkelsatzes ist <)BPD = α. Außerdem ist <)UPZ = <)VPW = α (als Normalwinkel zu α bzw. γ; bekanntlich ergänzen einander die gegenüberliegenden Winkel in einem Sehnenviereck auf 180°.) Daher sind die Vierecke PUBV und PZDW ähnlich, und es gilt
u : v = z : w
, was zu beweisen war.
Zur Verallgemeinerung auf einen beliebigen Kegelschnitt formen wir diesen Ausdruck noch etwas um:
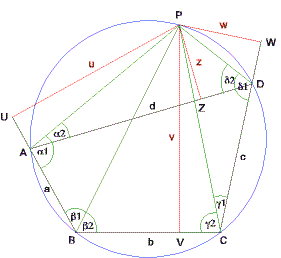
Aus dem Sinussatz erhalten wir:
und analog 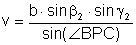 ,
,
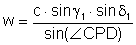 ,
, 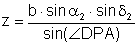 .
.
Außerdem können wir zeigen:
und analog
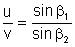 ,
,
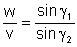 ,
, 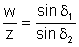 .
.
Setzen wir 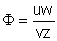 und setzen ein, so erhalten wir
und setzen ein, so erhalten wir
Der zweite Bruch ist aber das Doppelverhältnis der Geraden PA, PC, PB, PD. Es ist also
Bei einer projektiven Transformation ändert sich dieses Verhältnis nur um einen konstanten Faktor (den Faktor, um den sich bd/ac ändert - das Doppelverhältnis bleibt gleich). Da jeder Kegelschnitt durch eine projektive Transformation in einen Kreis übergeführt werden kann, ist die Behauptung gezeigt.