3. Die Mittelpunktsgleichung von Ellipse und Hyperbel

Aus den klassischen Definitionen können wir leicht die heute üblichen Gleichungen für Ellipse und Hyperbel ableiten.

Wir legen den Mittelpunkt der Ellipse in den Koordinatenursprung und die Hauptachse in Richtung der x-Achse (das bezeichnet man als 1. Hauptlage - bei der 2. Hauptlage liegt die Hauptachse in Richtung der y-Achse). Dann lautet die Gleichung in heutiger Schreibweise:

Das können wir umformen zur Normalform

b²x² + a²y² = a²b²

bzw.

(Für a = b = r ergibt sich die Kreisgleichung: x² + y² = r²)

Für die Hyperbel erhalten wir ebenso

,

wobei c eine Konstante ist.

Setzen wir analog zur Ellipsengleichung die rechte Seite gleich 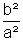und formen um, so erhalten wir die Hyperbelgleichung

b²x² - a²y² = a²b²

bzw.

Jetzt müssen wir noch beweisen, dass wir für b denselben Wert erhalten, den wir in Abschnitt 1.2 definiert haben. Dazu legen wir eine Gerade durch den Ursprung und einen beliebigen Hyperbelpunkt P(x/y). Die Steigung dieser Geraden ist dann 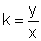. Aus der Hyperbelgleichung erhalten wir

, also .

Wenn x gegen Unendlich geht, geht der Ausdruck in der Klammer gegen 1. Wir erhalten daher für die Steigung der Asymptoten:

bzw. ,

und das stimmt genau mit unserer ursprünglichen Definition überein.

(1. und 2. Hauptlage ist ebenso wie bei der Ellipse definiert.)

Ellipse und Hyperbel bezeichnet man auch als Mittelpunktskegelschnitte. Aus den Gleichungen folgt, dass diese Kurven zu ihren Achsen symmetrisch sind (wie in 1.2 behauptet), denn mit einem beliebigen Punkt P(x/y) erfüllen auch die dazu symmetrischen Punkte (±x/±y) die Gleichung.

Inhalt - Zurück - Weiter: Scheitelgleichung