Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Die Parabel hat keinen Mittelpunkt. Wir legen daher den Scheitel in den
Koordinatenursprung und die Achse in Richtung der x-Achse. Dann lautet die Gleichung:
.
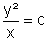Die Konstante bezeichnet man mit 2p (manchmal auch nur p). Dabei ist p der sogenannte Parameter der Parabel. Wir erhalten daher als Normalform der Parabelgleichung in 1. Hauptlage
|
y² = 2px |
(Bei der 2. Hauptlage liegt die Achse in Richtung der y-Achse.)
Wir können natürlich auch eine Ellipse oder Hyperbel so in ein Koordinatensystem einzeichnen, dass ein Scheitel im Ursprung liegt. Die entsprechenden Gleichungen lauten dann
bzw.
Das können wir umformen zu
Damit alle drei Gleichungen eine einheitliche Gestalt bekommen, setzen wir
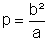und erhalten als Scheitelgleichung
|
|
(das Vorzeichen - gilt für die Ellipse, + für die Hyperbel). Die Parabel ist der Grenzfall für a gegen unendlich, wir können daher p/a gleich 0 setzen.
Die Abbildung zeigt eine Ellipse, eine Parabel und eine Hyperbel in Scheitellage, die den selben Parameter haben:
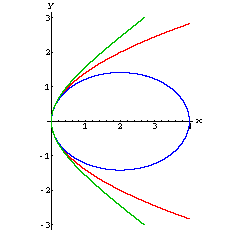
Diese Gleichungen entsprechen im Wesentlichen der Form, in der Apollonius von Perge die "Symptome" der Kegelschnitte angibt. Er benutzt dabei Ausdrücke aus der Theorie der Flächenanlegung, die den griechischen Mathematikern seit Pythagoras und Euklid geläufig war:
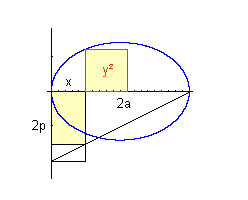
Wir zeichnen im Scheitel eines Kegelschnitts, normal auf die Achse, eine Strecke der Länge 2p. Für einen beliebigen Punkt betrachten wir jetzt das Rechteck mit den Seitenlängen 2p und x sowie das Quadrat über y.
 |
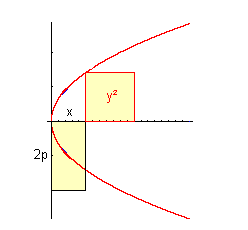Da für die Parabel gilt: y² = 2px, haben das Quadrat und das Rechteck den gleichen Flächeninhalt. Das kann man als "parabolische" Flächenanlegung auffassen (von paraballein = gleichkommen). (Vergleiche dazu das Applet auf http://members.aol.com/geometrie11/koorgeom/parzirli.htm.) |
 |
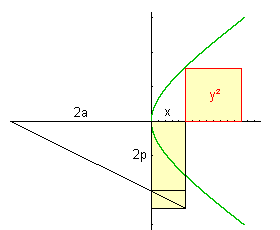
Bei der Ellipse fehlt dem Quadrat etwas zur Fläche des Rechtecks, und zwar ein Rechteck, dessen Seiten sich wie p:a verhalten. Es handelt sich also um eine "elliptische" Flächenanlegung (von elleipein = ermangeln, fehlen). |
 |
Im Fall der Hyperbel übertrifft das Quadrat die Fläche des Rechtecks, es liegt also eine "hyperbolische" Flächenanlegung vor (von hyperballein = übertreffen). (Das Applet für diese beiden Fälle gibt es auf http://members.aol.com/geometrie11/koorgeom/apolloni.htm - liegt der Punkt R rechts von O, erhält man eine Ellipse, sonst eine Hyperbel.) |
Das ist also der Grund, dass Apollonius den Kegelschnitten die bis heute üblichen Namen gab.
Wir betrachten jetzt eine Kegelschnitt in Scheitellage und einen Kreis, der ihn im Scheitel berührt. Der Mittelpunkt des Kreises muss also auf der x-Achse liegen, und die Kreisgleichung lautet:
(x - r)² + y² = p² bzw. y² = 2rx - x²
Wir bringen beide Kurven zum Schnitt:
Eine Lösung dieser Gleichung lautet x = 0 (weil ja beide Kurven durch den Koordinatenursprung gehen). Für r = p ist das die einzige Lösung. Im Allgemeinen können ein Kegelschnitt und ein Kreis bis zu 4 Schnittpunkte haben. Diese 4 Punkte fallen hier alle in einen zusammen. Ein Kreis, dessen Radius gleich dem Parameter des Kegelschnitts ist, schmiegt sich also im Scheitel besonders gut an - er hat an dieser Stelle die selbe Krümmung wie der Kegelschnitt. Einen solchen Kreis bezeichnet man daher als Scheitelschmiegkreis oder Scheitelkrümmungskreis.
Zur Erinnerung: Bei der Ellipse und Hyperbel ist .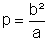
Die Krümmungskreise in den Nebenscheiteln einer Ellipse haben den Radius
.
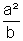Diese Kreise sind eine große Hilfe beim Zeichnen eines Kegelschnitts. Ihre Mittelpunkte können folgendermaßen konstruiert werden:
|
|
