5. Kegelschnitte und ihre Brennpunkte

5.1. Die Brennpunktseigenschaft

Im Schulunterricht werden die Kegelschnitte meist anders definiert:

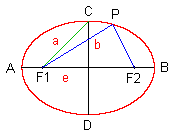	Angenommen, es sind zwei Punkte F1 und F2 (die Brennpunkte) gegeben; ihr Abstand beträgt 2e. Dann besteht die Ellipse aus allen Punkten P der Ebene, für die die Summe der Abstände PF1 und PF2 konstant ist: ell = {P / PF1 + PF2 = 2a} Dabei gilt, wie man z.B. aus dem rechtwinkeligen Dreieck OF1C ablesen kann: e² = a² - b² Die Strecken PF1 und PF2 bezeichnet man als Leit- oder Brennstrahlen. Das Verhältnis heißt numerische Exzentrizität; bei der Ellipse ist ε < 1.
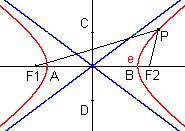	Die Hyperbel ist die Menge aller Punkte P der Ebene, für die die Differenz der Abstände PF1 und PF2 konstant ist: hyp = {P / |PF1 - PF2| = 2a} Dabei ist e² = a² + b² ε definiert man wie oben; bei der Hyperbel gilt ε > 1.
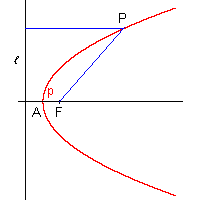	Die Parabel schließlich besteht aus allen Punkten, die von einem Brennpunkt F und einer Leitlinie ℓ gleich weit entfernt sind: par = {P / PF = Pℓ} Dabei ist der Abstand des Brenpunkts von der Leitlinie gleich p, dem Parameter der Parabel.

Mithilfe der Brennpunktseigenschaften kann man die Kegelschnitte punktweise konstruieren.

Geometrischer Beweis

Wir müssen jetzt zeigen, dass wir mit diesen Definitionen dieselben Kurven erhalten wie vorhin. Der belgische Ingenieur Pierre Dandelin (1794 - 1847) hat dafür einen wunderschönen Beweis gefunden:

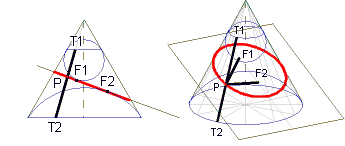
Zuerst betrachten wir den Fall, dass ein Drehkegel von einer Ebene in einer Ellipse geschnitten wird. Wir schreiben in den Kegel zwei Kugeln ein, die ihren Mittelpunkt auf der Kegelachse haben und die Schnittebene in den Punkten F₁ bzw. F₂ berühren. Da alle Tangentenstrecken von einem Punkt an eine Kugel gleich lang sind, gilt für einen beliebigen Ellipsenpunkt P:

PF₁ + PF₂ = PT₁ + PT₂ = T₁T₂,

und wie man auf der Zeichnung sieht, ist das konstant.

Für die Hyperbel verläuft der Beweis ganz analog.

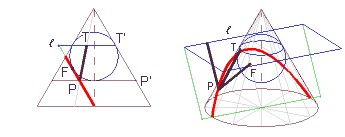
Bei der Parabel gibt es nur eine Dandelin-Kugel. Wenn wir die Ebene, in der diese Kugel den Kegel berührt, mit der Parabelebene schneiden, erhalten wir die Leitlinie der Parabel, denn

PF = PT = P'T' = Pℓ

Analytischer Beweis

Bei einer Ellipse in Mittelpunktslage haben die Brennpunkte die Koordinaten F₁(-e/0) und F₂(e/0). Daraus können wir die Abstände PF₁ bzw. PF₂ berechnen:

(das Vorzeichen + gilt für PF₁, das - für PF₂). Wenn man das ausmultipliziert und berücksichtigt, dass e² = a² - b², erhält man

PF = a ± εx und PF₁ + PF₂ = 2a

Für die Hyperbel finden wir ganz analog:

PF = |εx ± a| und |PF₁ - PF₂| = 2a.

Da der Scheitel einer Parabel den Abstand Brennpunkt - Leitlinie halbiert, hat der Brennpunkt die Koordinaten 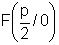und die Leitlinie die Gleichung 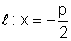. Daher ist

5.2. Fadenkonstruktionen

Man kann die Kegelschnitte konstruieren, indem man die Brennpunktseigenschaften ausnützt.

Die "Gärtnerkonstruktion" der Ellipse war schon Themios von Tralleis (ca. 500 n. Chr.), dem Erbauer der Hagia Sophia, bekannt: Man befestigt die Enden einer Schnur der Länge 2a in den Brennpunkten und fährt mit einem Bleistift an der straff gespannten Schnur entlang. (Ein Applet dazu findest du auf http://members.aol.com/geometrie11/koorgeom/elli1.htm - klicke auf "Brennstrecken ein".)

Für einen Hyperbelzirkel bindet man ein Ende der Schnur an ein Lineal, das um 2a länger ist als die Schnur. Das Ende des Lineals kann sich um den einen Brennpunkt drehen, das andere Ende der Schnur wird im zweiten Brennpunkt befestigt. Jetzt muss man den Bleistift so halten, dass er immer am Lineal entlanggleitet und die Schnur gespannt bleibt. Dann beschreibt er einen Hyperbelast. (Veranschaulichung: http://members.aol.com/geometrie11/koorgeom/hypfaden.htm)

Für einen Parabelzirkel braucht man zwei Lineale: eines markiert die Leitlinie, das andere, an dem die Schnur befestigt ist, gleitet im rechten Winkel daran entlang. Die Schnur ist genauso lang wie das zweite Lineal, ihr anderes Ende wird wieder im Brennpunkt befestigt. (Veranschaulichung: http://members.aol.com/geometrie11/koorgeom/parfaden.html)

5.3. Die Bedeutung von p und ε

Den Parameter p haben wir zuerst willkürlich definiert. Jetzt können wir ihn auch direkt aus dem Kegelschnitt ablesen. Eine Sehne, die durch einen Brennpunkt geht und normal auf die Achse steht, hat nämlich die Länge 2p. (Das kann man leicht nachrechnen.)

ε, die numerische Exzentrizität, ist ein Maß dafür, wie sehr ein Kegelschnitt vom Kreis abweicht. Für den Kreis ist ε = 0. Wie erwähnt, ist bei der Ellipse ε < 1, bei der Hyperbel ε > 1. Für die Parabel setzen wir ε = 1.

Den Koeffizienten 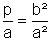, der bei der Scheitelgleichung auftritt, können wir auch durch ε ausdrücken. Für die Ellipse ergibt sich 1 - ε², für die Hyperbel ε² - 1. Daher können wir alle drei Arten von Kegelschnitten durch eine einzige Scheitelgleichung beschreiben:

In Abschnitt 1 haben wir einen Kegel mit dem halben Öffnungswinkel φ mit einer Ebene geschnitten, die mit der Kegelachse den Winkel ω einschließt. Die Exzentrizität des dabei entstehenden Kegelschnitts ist

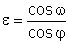
Beweis:

Für die Parabel ist der Satz klar, weil ω = φ.

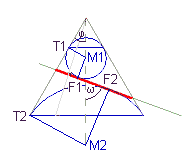Um die Beziehung für die Ellipse zu zeigen, betrachten wir noch einmal das Bild mit den Dandelin-Kugeln. Ihre Mittelpunkte bezeichnen wir mit M₁ und M₂. Wenn wir die Verbindungsstrecke M₁M₂ einmal auf die Schnittebene und einmal auf die Mantellinie des Kegels projizieren, erhalten wir

2e = F₁F₂ = M₁M₂·cos ω

2a = T₁T₂ = M₁M₂·cos φ

Jetzt müssen wir nur noch die erste Gleichung durch die zweite dividieren und erhalten die angegebene Formel.

Inhalt - Zurück - Weiter: Tangenten