6. Tangenten an Kegelschnitte

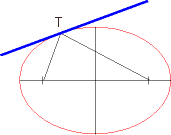
Als Tangente an einen Kegelschnitt im Punkt T bezeichnet man eine Gerade, die mit der Kurve nur den Punkt T gemeinsam hat. (Das trifft allerdings auch für eine Gerade zu, die zur Achse einer Parabel parallel ist. Um diesen Fall auszuschließen, muss man noch fordern, dass alle Punkte der Geraden auf derselben Seite des Kegelschnitts liegen.)

Die Gleichung der Tangente an einen Kegelschnitt in 1. Hauptlage im Punkt T(x_T/y_T) lautet für die

Ellipse: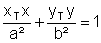
Hyperbel: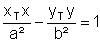
Parabel:	yTy = p·(x + xT)

Das beweist man am besten, indem man die Kegelschnittsgleichungen implizit differenziert.

(Für einen Kreis erhalten wir: x_Tx + y_Ty = r².)

Am einfachsten merkt man sich folgende Regel: schreibe in der Kegelschnittsgleichung x·x für x², y·y für y² und x + x für 2x und ersetze dann jeweils eine Variable durch die entsprechende Koordinate des Berührpunkts.

Für die geometrische Konstruktion ist es gut zu wissen, dass die Tangente den Winkel zwischen den Leitstrahlen halbiert (bei der Ellipse den Außenwinkel, bei Hyperbel und Parabel den Innenwinkel).

Das bedeutet: Stellt man sich die Ellipse als Spiegel vor und stellt in den einen Brennpunkt eine Lichtquelle, dann reffen sich die reflektierten Strahlen im zweiten Brennpunkt (daher der Name "Brennpunkt".) Bei der Hyperbel scheinen die reflektierten Strahlen vom zweiten Brennpunkt auszugehen; bei der Parabel werden Strahlen, die parallel zur Achse einfallen, in den Brennpunkt reflektiert.

Schon Diokles, ein Zeitgenosse von Apollonius, schlug vor, mit Parabolspiegeln die Opferfeuer in Tempeln zu entzünden, um die Leute zum Staunen zu bringen. Im Mittelalter konstruierte man nach diesem Prinzip Flüstergewölbe (wer in einem Brennpunkt steht, kann alles hören, was im anderen Brennpunkt gesprochen wird). Heute verwendet man es zum Beispiel für Autoscheinwerfer, Parabolantennen und Nierensteinzertrümmerer. Auch darüber findest du interessante Informationen auf http://members.aol.com/geometrie11/.

Außerdem folgt aus dieser Eigenschaft, dass konfokale Kegelschnitte (eine Ellipse und eine Hyperbel, die dieselben Brennpunkte besitzen) einander immer im rechten Winkel schneiden.

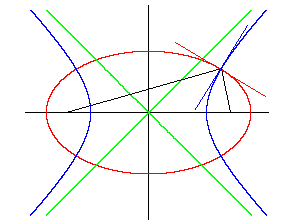
Beweis:

Ich führe den Beweis nur für die Ellipse durch.

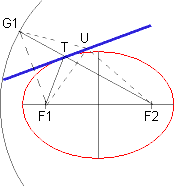
Wir zeichnen um den Brennpunkt F₂ einen Kreis mit dem Radius 2a, den 1. Leitkreis. G₁, den Schnittpunkt der Verlängerung von F₂T mit dem Kreis bezeichnet man als 1. Gegenpunkt von T. Wie man sieht, ist TF₁ = TG₁. Der Leitkreis entspricht also der Leitlinie einer Parabel.

Jetzt zeichnen wir die Symmetrale der Strecke F₁G₁; sie halbiert gleichzeitig den Winkel F₁TG₁. Für einen beliebigen, von T verschiedenen Punkt U auf dieser Geraden gilt: UF₁ + UF₂ = UG₁ + UF₂ > 2a; er kann also nicht auf der Ellipse liegen, und die Gerade ist tatsächlich eine Tangente.

Der Beweis zeigt gleichzeitig, wie die Konstruktion der Tangente praktisch durchgeführt werden kann. Natürlich kann man ebenso den 2. Leitkreis mit F₁ als Mittelpunkt verwenden.

Außerdem erhalten wir daraus eine weitere Konstruktion, die Faltkonstruktion der Kegelschnitte:

Wir zeichnen auf ein Blatt Papier einen Kreis und einen Punkt. Nun falten wir das Papier immer wieder so, dass der Punkt auf dem Kreisumfang zu liegen kommt. Liegt der Punkt innerhalb des Kreises, so hüllen die Falten eine Ellipse ein; liegt er außerhalb, ergibt sich eine Hyperbel; und wenn wir statt des Kreises eine Gerade verwenden, erhalten wir eine Parabel. (Siehe dazu die Applets "Parabel, Ellipse, Hyperbel als Hüllkurve" auf http://members.aol.com/geometrie11/.)

Inhalt - Zurück - Weiter: Leitlinien, Polargleichung