Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Daraus erhalten wir eine weitere gemeinsame Definition der Kegelschnitte:
Ein Kegelschnitt ist die Menge aller Punkte der Ebene, für die das Verhältnis der Abstände zum Brennpunkt und zur Leitlinie konstant ist.
k = {P / PF = ε·Pℓ}
Geometrischer Beweis:
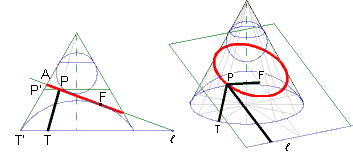
Die Zeichnung zeigt nur die Leitlinie, die zum unteren Brennpunkt gehört. Es ist
Aus dem Sinussatz folgt
Analytischer Beweis
Für die Parabel haben wir die Aussage bereits bewiesen.
Wie wir in 5.1 gezeigt haben, gilt für einen Ellipsenpunkt: PF = a ± εx. Das können wir umformen zu
.
Die Leitlinien sind also die die Geraden mit der Gleichung
(Das Vorzeichen + gilt dabei für den linken Brennpunkt und die dazugehörige Leitlinie, das - für den rechten.).
Für die Hyperbel gilt
,
wobei sich für die Leitlinien dieselben Gleichungen ergeben wie bei der Ellipse.
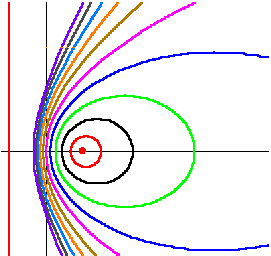
Die Abbildung zeigt einige Kegelschnitte, die einen Brennpunkt und die dazugehörige Leitlinie gemeinsam haben.
Die obige Beziehung können wir auch in Polarkoordinaten ausdrücken, wobei wir einen Brennpunkt als Pol wählen. (Eine Einführung in Polarkoordinaten findet sich auf http://www.mathe-online.at/mathint/zeich/i.html#Polarkoordinaten.)
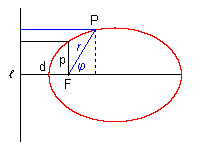
Wir betrachten zunächst eine Ellipse und wählen den linken Brennpunkt als Pol. Die folgenden Überlegungen gelten aber für alle Kegelschnitte, weil die Leitliniendefinition ja allen gemeinsam ist. Wir können sie auch schreiben als
r = ε·(d + r·cos φ),
wobei d der Abstand vom Brennpunkt zur Leitlinie ist. Setzen wir φ = 90°, erhalten wir p = ε·d, die obige Gleichung wird also zu
r = p + ε·r·cos φ
Daraus berechnen wir r und erhalten als Gleichung der Kegelschnitte in Polarkoordinaten:
|
|
Wählt man den rechten Brennpunkt als Pol, so lautet die Gleichung
.
(Wenn man den Pol in den Mittelpunkt legt, erhält man für die Ellipse die Gleichung
und für die Hyperbel
.)