8. Weitere Formeln

Einige Formeln möchte ich hier noch - der Vollständigkeit halber - ohne Beweis anführen.

8.1. Die Gleichungen der Kegelschnitte in Parameterdarstellung

Einen weitere Möglichkeit, eine Kurve zu beschreiben, ist die Parameterdarstellung. Dabei wird die Beziehung zwischen den Koordinaten eines Punktes nicht durch eine einzige Gleichung angegeben, sondern x und y werden durch eine veränderliche Größe, den Parameter t, ausgedrückt (nicht zu verwechseln mit dem Parameter p der Kegelschnitte.)

Eine Parameterdarstellung des Kreises lautet z.B.

x = r·cos t
y = r·sin t       0 ≤ t < 2π

Daraus erhalten wir als Parameterdarstellung einer Ellipse in 1. Hauptlage:

x = a·cos t
y = b·sin t       0 ≤ t < 2π

Umgekehrt kann man den Parameter, der zu einem Ellipsenpunkt P(x/y) gehört, berechnen: .

Für die Hyperbel erhält man eine ganz ähnliche Darstellung, wenn man die Hyperbelfunktionen Sinus hyperbolicus und Cosinus hyperbolicus benutzt. Sie werden folgendermaßen definiert:

.

Die Bezeichnungen kommen daher, dass diese Funktionen viele ähnliche Eigenschaften wie die Sinus- und Cosinusfunktion haben. (So gilt z.B. cosh² x - sinh² x = 1, ähnlich wie cos² x + sin² x = 1.)) Die Parameterdarstellung einer Hyperbel in 1. Hauptlage (genauer gesagt, des rechten Hyperbelastes) lautet nun

x = a·cosh t
y = b·sinh t       -∞ < t < ∞

Den Parameterwert zu einem Hyperbelpunkt P(x/y) erhält man aus der Gleichung .

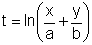Für die Parabel sind verschiedene Parametrisierungen denkbar, z.B.

,       y = pt       -∞ < t < ∞

8.2. Flächeninhalte

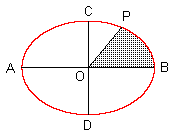	Der Flächeninhalt der Ellipse beträgt A = abπ       (siehe auch 10.1) Der Flächeninhalt des Ellipsensektors OBP beträgt , wobei t der Parameterwert des Punktes P ist, wie oben angegeben.
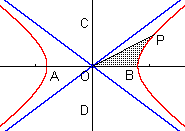	Ebenso erhält man für den Hyperbelsektor OBP .

(Anmerkung: Die Umkehrfunktionen der Hyperbelfunktionen heißen Areasinus bzw. Areacosinus hyperbolicus - von Area = Fläche - , abgekürzt arsinh und arcosh, weil t in der Formel für den Flächeninhalt des Hyperbelsektors auftritt.)

Der Flächeninhalt eines Parabelsegments beträgt, wie Archimedes als erster gezeigt hat, 4/3 der Fläche des größten eingeschriebenen Dreiecks (siehe 12.1 ). Daraus erhält man für ein Segment einer Parabel in 1. Hauptlage, das von der Sehne zwischen den Punkten (x₁/y₁) und (x₂/y₂) b egrenzt wird, den Flächeninhalt

8.3. Bogenlängen

Die Bogenlängen der Kegelschnitte sind sehr kompliziert zu berechnen.

Wenn wir für die Parabel die oben angegebene Parameterdarstellung wählen, erhalten wir für die Länge des Parabelbogens zwischen den Parameterwerten 0 und t

Wenn wir versuchen, die Bogenlänge einer Ellipse oder Hyperbel zu berechnen, kommen wir auf die Integrale 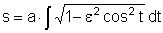(für die Ellipse) bzw. 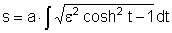(für die Hyperbel). Diese Ausdrücke führen auf sogenannte elliptische Integrale, die nicht exakt gelöst werden können. Man kann sie nur näherungsweise berechnen.

Inhalt - Zurück - Weiter: Allgemeine Lage