10. Affine Eigenschaften der Kegelschnitte

Stellen wir uns vor, eine ebene Figur wirft ihren Schatten auf eine andere Ebene. Die Lichtstrahlen nehmen wir als parallel an, man spricht daher von einer Parallelprojektion. Der Schatten ist dann ein verzerrtes Bild der ursprünglichen Figur, aber einige Eigenschaften bleiben erhalten: parallele Gerade bleiben parallel, gleichgroße Flächen bleiben gleich groß, und wenn ein Punkt eine Strecke in einem bestimmten Verhältnis teilt, tut er das auch im Schatten.

Eine solche Abbildung bezeichnet man als affine Transformation. Die affine Geometrie beschäftigt sich mit denjenigen geometrischen Eigenschaften, die dabei erhalten bleiben. Man kann es auch so ausdrücken: affine Eigenschaften bleiben erhalten, wenn man von rechtwinkeligen zu schiefwinkeligen Koordinaten übergeht oder die Maßstäbe auf den Koordinatenachsen verändert (zu schiefwinkeligen Koordinaten siehe http://www.mathe-online.at/mathint/zeich/i.html#schiefwK).

Eine affine Transformation führt einen Kegelschnitt in einen Kegelschnitt gleichen Typs über. Wir können daher manche Eigenschaften bewiesen, indem wir eine besonders günstige Lage des Kegelschnitts wählen (z.B. einen Kreis statt einer Ellipse).

10.1. Die Ellipse als affines Bild des Kreises

Da auch alle Flächen im Verhältnis b/a verkleinert werden, erhält man die schon in 8.2. erwähnte Formel für den Flächeninhalt der Ellipse: A = abπ.

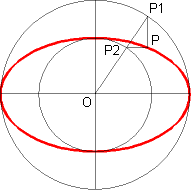	Aufgrund dieser Eigenschaft können wir die Ellipse punktweise konstruieren, wie in der Abbildung gezeigt (Konstruktion nach Proklos): man zeichnet einen Radius, der die beiden Kreise in P1 bzw. P2 schneidet, zieht durch P1 eine Parallele zur y-Achse und durch P2 eine Parallele zur x-Achse. Der Schnittpunkt dieser beiden Geraden liegt dann auf der Ellipse.
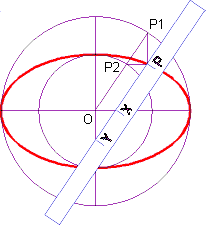	Wir können diese Konstruktion noch verbessern, indem wir durch P eine Parallele zum Radius zeichnen. X und Y seien ihre Schnittpunkte mit den Koordinatenachsen. Dann ist XP = OP2 = b und YP = OP1 = a. Wir können also auf einem Papierstreifen oder einem Lineal die Strecken YX = a - b und XP = b markieren. Wenn wir das Lineal dann so bewegen, dass X auf der x-Achse und Y auf der y-Achse gleitet, beschreibt der Punkt P eine Ellipse. Diese Konstruktion heißt 1. Papierstreifenkonstruktion der Ellipse.
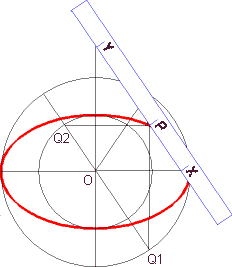	Diese Konstruktion wird allerdings sehr ungenau, wenn x - y sehr klein ist. In solchen Fälle kann man die 2. Papierstreifenkonstruktion anwenden. Dazu betrachten wir die zu P1 bzw. P2 symmetrischen Punkte Q1 und Q2. Es ist XP = OQ2 = b und YP = OQ1 = a. Wir erhalten also wieder eine Ellipse, wenn wir X und Y auf den Koordinatenachsen gleiten lassen.

Nach dem Prinzip dieser beiden Konstruktionen kann man auch Ellipsenzirkel konstruieren. Siehe auch die Applets auf http://members.aol.com/geometrie11/koorgeom/ellzir2.htm und http://members.aol.com/geometrie11/koorgeom/ellzir3.htm.

10.2. Konjugierte Durchmesser

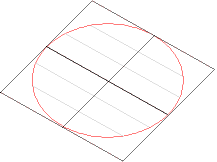
Zwei Durchmesser eines Kreises, die aufeinander normal stehen, haben folgende Eigenschaften:

• Ein Durchmesser ist parallel zu den Tangenten in den Endpunkten des anderen Durchmessers.
• Ein Durchmesser halbiert alle Sehnen, die zum anderen Durchmesser parallel sind.

Bildet man einen Kreis durch eine affine Transformation auf eine Ellipse ab, bleiben diese Eigenschaften erhalten. Die entsprechenden Durchmesser stehen dann aber im Allgemeinen nicht mehr normal aufeinander. Man bezeichnet sie als konjugierte Durchmesser. (Die einzigen konjugierten Durchmesser, die einen rechten Winkel einschließen, sind die Achsen.)

Sind k₁ und k₂ die Steigungen zweier konjugierter Durchmesser einer Ellipse in erster Hauptlage, so gilt

Das Viereck, das durch die Tangenten gebildet wird, hat den konstanten Flächeninhalt 4ab. Auch das Viereck, dessen Ecken die Endpunkte der konjugierten Durchmesser sind, hat konstanten Flächeninhalt, und zwar 2ab. Das kann man sich leicht anhand der Situation beim Kreis überlegen; bei einer affinen Transformation bleiben gleichgroße Flächen gleich groß.

Auch bei der Hyperbel sind konjugierte Durchmesser dadurch charakterisiert, dass der eine parallel ist zu den Tangenten in den Endpunkten des anderen. Allerdings schneidet nur einer der beiden Durchmesser die Hyperbel. (Die Asymptoten kann man auffassen als Durchmesser, die zu sich selbst konjugiert sind.)

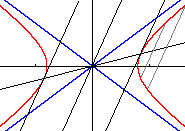
Die Beziehung zwischen den Steigungen lautet

Bei der Parabel sind alle Durchmesser zur Achse parallel. Es gibt daher zu einem Durchmesser nur eine konjugierte Sehnenrichtung.

10.3. Einige Eigenschaften der Hyperbel

Verwendet man schiefwinkelige Koordinaten, so beschreibt diese Gleichung ebenfalls eine Hyperbel. Man kann also jede Hyperbel in dieser Form darstellen, wenn man ihre Asymptoten als Achsen eines schiefwinkeligen Koordinatensystems wählt.

Das können wir ausnützen, um einige interessante Eigenschaften der Hyperbel zu beweisen, die ebenfalls schon bei Apollonius erwähnt werden:

• Der Abschnitt einer beliebigen Hyperbeltangente, der zwischen den Asymptoten liegt, wird vom Berührpunkt halbiert.
• Das Dreieck, das vom Tangentenabschnitt und den Asymptoten begrenzt wird, hat konstanten Flächeninhalt.
• Wenn eine Gerade die Hyperbel in zwei Punkten schneidet, sind die Abschnitte zwischen den Schnittpunkten und den Asymptoten gleich lang.

Es genügt, diese Eigenschaften für die Hyperbel mit der Gleichung xy = c zu beweisen. Ich werde nur die erste Eigenschaft zeigen (die anderen Beweise überlasse ich dem Leser).

Sei P(x₀/y₀) ein Punkt der Hyperbel. Wir ziehen eine Gerade durch die Punkte (2x₀/0) und (0/2y₀). Diese Gerade geht durch P; die Strecke zwischen den Koordinatenachsen wird von P halbiert. Die Gleichung der Geraden lautet in Parameterform: x = x₀ + t·x₀, y = y₀ - t·y₀. Für einen von P verschiedenen Punkt der Geraden ist daher

Es kann daher kein weiterer Hyperbelpunkt auf der Geraden liegen, und es handelt sich tatsächlich um eine Tangente.

Inhalt - Zurück - Weiter: Projektive Eigenschaften