11. Projektive Eigenschaften der Kegelschnitte

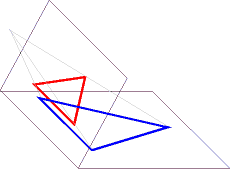
Wir betrachten wieder den Schatten einer ebenen Figur auf einer anderen Ebene, aber diesmal gehen die Lichtstrahlen von einem Punkt aus. Das bezeichnet man als Zentralprojektion. Dieselbe Situation liegt vor, wenn wir ein Bild mit korrekter Perspektive malen. Dabei werden die Sehstrahlen, die vom Auge ausgehen, mit der Bildebene (der Leinwand) geschnitten. Albrecht Dürer (1471 - 1528) hat sich viel mit Perspektive beschäftigt; das Bild aus seiner Schrift "Underweysung der messung mit dem zirckel und richtscheyt..." stellt das Prinzip dar:

Bei dieser Abbildung gehen parallele Geraden im Allgemeinen in schneidende über. Wir alle wissen, wie sich z.B. Eisenbahnschienen auf einem Bild scheinbar schneiden. Wir denken uns daher zu jeder Schar paralleler Geraden einen unendlich fernen Punkt, den Fernpunkt. Die Menge aller Fernpunkte bildet die Ferngerade. Dadurch wird die Ebene zur projektiven Ebene erweitert.

Auch Teilverhältnisse bleiben bei einer Zentralprojektion nicht erhalten, wohl aber das Doppelverhältnis von vier Punkten. Es wird folgendermaßen definiert: Liegen die Punkte A, B, X und Y auf einer Geraden, so ist ihr Doppelverhältnis

Dabei betrachtet man die Strecken als gerichtete Strecken, das heißt, wenn X nicht zwischen A und B liegt, ist AX/XB negativ. Einer der Punkte kann auch ein Fernpunkt sein; ist z.B. X ein Fernpunkt, so ist AX/XB = -1.

Wenn vier Geraden durch einen Punkte gehen, definiert man ihr Doppelverhältnis als das Doppelverhältnis ihrer Schnittpunkte mit einer beliebigen weiteren Geraden.

Vier Punkte heißen harmonisch, wenn ihr Doppelverhältnis -1 beträgt. Dann teilt z.B. X die Strecke AB von innen im selben Verhältnis wie Y von außen.

Abbildung, bei denen das Doppelverhältnis erhalten bleibt, heißen projektive Transformationen. Die projektive Geometrie beschäftigt sich mit den geometrische Eigenschaften, die bei projektiven Transformationen erhalten bleiben.

Jetzt nehmen wir an, dass die abgebildete Figur ein Kreis ist. Die Sehstrahlen bilden dann einen Kegel, und der Schnitt mit der Bildebene ist ein Kegelschnitt - eine Ellipse, Parabel oder Hyperbel, je nachdem, ob er mit der Ferngerade 0, 1 oder 2 Punkte gemeinsam hat. Verallgemeinernd können wir feststellen, dass ein Kegelschnitt durch eine projektive Abbildung wieder auf einen Kegelschnitt abgebildet wird. Bei manchen Eigenschaften genügt es daher, sie für den Kreis zu beweisen.

11.1. Der Satz von Pascal

Blaise Pascal (1623 - 1662) veröffentlichte mit 16 Jahren eine Abhandlung über Kegelschnitte. Darin bewies er folgenden Satz:

Schreibt man einem Kegelschnitt ein Sechseck ein, so liegen die Schnittpunkte je zweier gegenüberliegender Seiten (also der Schnittpunkt von AB und DE, von BC und EF und von CD und FA) auf einer Geraden.

Das Applet Pascal zeigt die Situation für einen Kreis. Ein Beweis findet sich z.B. auf http://www.madincea.privat.t-online.de/aufg09.htm, Nr. 42. (Auf dieser Seite findet man auch alle Voraussetzungen, die für den Beweis benötigt werden.) Wenn wir den Kreis durch eine projektive Transformation auf einen Kegelschnitt abbilden, bleiben die Schnittpunkte von Geraden erhalten. Daher gilt der Satz auch für beliebige Kegelschnitte.

In Abschnitt 9 haben wir gesehen, dass ein Kegelschnitt durch 5 Punkte festgelegt ist. Mit Hilfe des Satzes von Pascal kann man weitere Punkte konstruieren. Das wird im Applet "5 Punkte" gezeigt. (Verschiebe die Punkte A bis E an beliebige Stellen. Dann drehe die rote Gerade, indem du am Punkt H ziehst. Der Punkt F beschreibt dann den Kegelschnitt.)

11.2. Pol und Polare

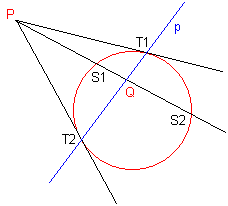Wir ziehen an einen Kreis in Mittelpunktslage von einem Punkt P(x_P/y_P) außerhalb des Kreises die Tangenten. Sie berühren den Kreis in den Punkten T₁(x₁/y₁) und T₂(x₂/y₂). Weil P auf beiden Tangenten liegt, gilt

x₁x_P + y₁y_P = rē und x₂x_P + y₂y_P = rē

Die Verbindungsgerade der beiden Berührpunkte hat daher die Gleichung

p: x_Px + y_Py = rē

Diese Gerade nennt man Polare von P. Ihre Gleichung wird genauso gebildet wie die Tangentengleichung. P ist der Pol von P.

Jetzt legen wir durch P eine beliebige Gerade, die den Kreis in S₁ und S₂ und p in Q schneidet. Man kann zeigen, dass die Punkte S₁, S₂, P und Q harmonisch liegen. Wir können daher die Polare auch so definieren:

Die Polare p des Punktes P enthält alle Punkte Q, für die gilt: Schneidet eine Gerade durch P den Kreis in S₁ und S₂, so ist Q der vierte harmonische Punkt zu S₁, S₂ und P.

Diese Definition ist auch dann sinnvoll, wenn P innerhalb des Kreises liegt. Die Pol-Polare-Beziehung ordnet also jedem Punkt der Ebene eine Gerade zu und umgekehrt. Wenn P auf dem Kreis liegt, ist die Polare die Tangente in P.

Wenn der Punkt Q auf der Polare p von P liegt, so liegt auch umgekehrt P auf der Polare q von Q. Man bezeichnet P und Q dann als konjugierte Punkte bzw. p und q als konjugierte Geraden.

Wenn wir nun den Kreis durch eine projektive Abbildung auf einen Kegelschnitt abbilden, bleiben Doppelverhältnisse erhalten. Wir können daher ebenso die Polare eines Punktes bezüglich eines Kegelschnitts definieren. Die Pol-Polare-Beziehung ist grundlegend für die Theorie der Kegelschnitte in der projektiven Geometrie. Viele schon bekannte Beziehungen können mit ihrer Hilfe ausgedrückt werden:

• Der Mittelpunkt eines Kegelschnitts ist der Pol der Ferngerade. (Bei der Parabel ist der Mittelpunkt selbst ein Fernpunkt.)

• Ist d ein Durchmesser eines Kegelschnitts, so ist die Polare seines Fernpunkts der zu d konjugierte Durchmesser.

• Die Brennpunkte eines Kegelschnitts sind diejenigen Punkte, in denen alle Paare von konjugierten Geraden normal aufeinander stehen.

• Die Leitlinien sind die Polaren der Brennpunkte.

Inhalt - Zurück - Weiter: Archimedes