Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Wie schon erwähnt, hat sich Archimedes (287 - 212 v. Chr.) ausführlich mit Kegelschnitten beschäftigt. Einige seiner Ergebnisse möchte ich hier vorstellen.
Bekanntlich gelang es den griechischen Mathematikern nicht, den Kreis zu quadrieren, das heißt, seinen Flächeninhalt exakt zu berechnen. Archimedes schaffte es aber, die Fläche eines Parabelsegments zu bestimmen. Auf diese Leistung war er zu Recht sehr stolz. Er fand folgende Regel ("Die Quadratur der Parabel", § 24):
"Der Inhalt eines Parabelsegments ist 4/3 des Inhalts des Dreiecks, das mit ihm gleiche Grundfläche und Höhe hat."
Archimedes gibt an, dass er die Lösung zuerst durch mechanische Überlegungen gefunden hat: Er zerlegt das Parabelsegment und ein Dreieck im Geist in schmale Streifen und untersucht, wie er diese an einem Waagebalken aufhängen muss, damit sie im Gleichgewicht sind. Da dieser Beweis aber Überlegungen verwendet, die nicht rein mathematisch sind, bestätigt er sein Ergebnis noch durch einen geometrischen Beweis.
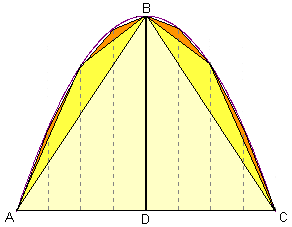
ABC sei das größte Dreieck, das dem gegebenen Segment einbeschrieben werden kann. (Archimedes führt den Beweis ganz allgemein für ein schräg abgeschnittenes Segment.) In jedem Fall ist die Tangente in B parallel zu AC, und der Durchmesser durch B halbiert die Basis AB in D. Den Flächeninhalt dieses Dreiecks bezeichnen wir mit Δ.
Den übrigbleibenden Parabelsegmenten werden wieder genau so Dreiecke einbeschrieben. Archimedes zeigt, dass die neuen Dreiecke zusammen 1/4 der Fläche des ersten Dreiecks haben. Wiederholt man diesen Vorgang, so kann man erreichen, dass die Restfläche beliebig klein wird.
Die Summe der Dreiecksflächen beträgt also Δ + 1/4·Δ + 1/16·Δ + ... In heutiger Ausdrucksweise würden wir sagen, dass die Summe dieser unendlichen geometrischen Reihe 4/3·Δ beträgt. In der Antike kannt man aber noch nicht die Begriffe "unendliche Reihe" und "Grenzwert". Archimedes zeigt daher durch eine doppelten Widerspruchsbeweis, dass die Fläche des Parabelsegments nicht größer, aber auch nicht kleiner als 4/3 der Dreiecksfläche betragen kann.
(Anmerkung: Diese Art von Beweis, eine Fläche durch eingeschriebene Flächen "auszuschöpfen", nennt man Exhaustionsmethode. Sie war bei den griechischen Mathematikern sehr beliebt und beruht auf einem Satz von Eudoxos von Knidos: "Zieht man von irgendeiner Größe einen Teil ab, der nicht kleiner als die Hälfte dieser Größe ist, vom Rest einen Teil, der nicht kleiner als die Hälfte ist, und so weiter, so bleibt schließlich eine Größe übrig, die kleiner als jede vorgegebenen Größe derselben Art ist.")
Das Hauptthema der Schrift "Über Paraboloide, Hyperboloide und Ellipsoide" sind die Rotationskörper, die entstehen, wenn sich ein Kegelschnitt um seine Achse dreht. Unter einem Hyperboloid versteht Archimedes allerdings nur den Teil, den man bei der Rotation eines Hyperbelastes um die Hauptachse erhält. Bei einem Ellipsoid ist dagegen Rotation um die große Achse (verlängertes Ellipsoid) oder um die kleine Achse (abgeplattetes Ellipsoid) möglich.
Archimedes untersucht nun die Segmente, die beim Schnitt dieser Körper mit einer Ebene entstehen. Er berechnet ihre Rauminhalte auf eine Art, die fast genau unserer Integralrechnung entspricht: Er zerlegt sie in dünne Schichten, denen er Zylinder ein- und umschreibt, und lässt dann die Dicke dieser Schichten beliebig klein werden.
Archimedes gibt das Volumen der Segmente im Verhältnis zu dem eines Kegels mit gleicher Grundfläche und Höhe an. Es gilt, wenn h die Höhe des Segmentes ist:
| Paraboloidsegment: | VSegment : VKegel = 3 : 2 |
| Hyperboloidsegment: | VSegment : VKegel = (3a + h) : (2a + h) |
| Ellipsoidsegment: | VSegment : VKegel = (3a - h) : (2a - h) |
| halbes Ellipsoid: | VSegment : VKegel = 2 : 1 |
Die Formel für das Paraboloid kann man auch so schreiben:
Aus der letzten Gleichung erhält man die Formel für das Ellipsoidvolumen: