13. Planetenbewegung und die Kepler'schen Gesetze

Johannes Kepler (1571 - 1630) untersuchte die Bewegung der Planeten. Seit der Antike waren Astronomen der Meinung, dass der Kreis die vollkommene Kurve sei und dass die Planetenbahnen daher aus Kreisbahnen zusammengesetzt sein müssten. Kepler erkannte nach langwierigen Berechnungen (auf der Grundlage der Beobachtungen von Tycho Brahe), dass das nicht stimmen konnte. Schließlich fand er die Regeln der Planetenbewegung, die man später in drei Gesetzen zusammengefasst hat:

1. Die Bahnen der Planeten sind Ellipsen, in deren einem Brennpunkt die Sonne steht.

2. Flächensatz: der Radiusvektor Sonne - Planet überstreicht in gleichen Zeiten gleiche Flächen.

3. Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben ihrer großen Halbachsen.

Aus den ersten beiden Gesetzen kann man schließen, dass die Planeten von einer Kraft bewegt werden, die immer zur Sonne zeigt (Zentralkraft) und umgekehrt proportional zum Quadrat der Entfernung ist. Das ist die Aussage des Gravitationsgesetzes von Isaac Newton (1643 - 1727). Umgekehrt erfolgt eine Bewegung um einen Zentralkörper, die dem Newton'schen Gravitationsgesetz gehorcht, immer auf einem Kegelschnitt. Je nach Anfangsgeschwindigkeit ist das eine Ellipse, eine Parabel oder eine Hyperbel. Eine geschlossene Bahn ergibt sich natürlich nur im ersten Fall.

In Wahrheit unterscheiden sich die Planetenbahnen nicht sehr von Kreisen. Kepler hatte Glück, dass er zuerst die Marsbahn untersuchte, deren Exzentrizität mit ε = 0,09 relativ groß ist. Für die Erde beträgt sie nur 0,016.

Für den Astronomen stellt sich jetzt die Aufgabe, die Position eines Planeten zu einer bestimmten Zeit zu berechnen. Das ist gar nicht so einfach. Kepler führte dazu verschiedene Hilfswinkel ein:

• Die wahre Anomalie φ ist der Winkel zwischen der Bahnachse und dem Planeten, von der Sonne aus gesehen (also der Winkel <)BSP in der Zeichnung - in der Astronomie wird der Bahnwinkel vom sonnennächsten Punkt der Bahn, dem Perihel, aus gemessen).

• Die exzentrische Anomalie η ist der Winkel zwischen der Bahnachse und der Projektion des Planeten auf einen der Bahn umschriebenen Kreis, vom Mittelpunkt der Bahn aus gesehen (also <)BOP').

• Die mittlere Anomalie μ ist der Winkel, den der Planet zurückgelegt hätte, wenn er sich mit gleichbleibender Geschwindigkeit auf einer Kreisbahn bewegen würde. Sie ist proportional zur verstrichenen Zeit, also nach dem 2. Gesetz proportional zur Fläche des Ellipsensektors SBP.

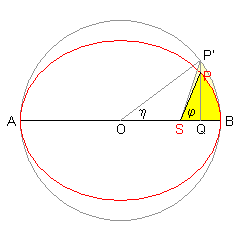
Wir müssen also das Verhältnis der Fläche SBP zur Ellipsenfläche berechnen. Das ist gleich dem Verhältnis von SBP' zur Kreisfläche:

μ : 2π = A(SBP) : A_Ellipse = A(SBP') : A_Kreis

Die Fläche SBP' besteht aus einem Kreissektor mit Zentriwinkel η, vermindert um ein Dreieck mit Grundlinie e und Höhe a sin η, ihr Inhalt beträgt daher

(wir haben e = ε·a eingesetzt).

Wenn wir das in die obere Proportion einsetzen, erhalten wir die Keplergleichung:

μ = η - ε·sin η

Diese Gleichung lässt sich nicht exakt nach η auflösen; man kann sie aber sehr gut näherungsweise lösen (siehe Fixpunktiteration).

Aus der exzentrischen Anomalie müssen wir jetzt noch die wahre Anomalie berechnen. Aus dem Dreieck SQP lesen wir ab: cos φ = SQ/SP. In 5.1. haben wir gezeigt: SP = a - εx; außerdem ist x = OQ = a·cos η. Wir erhalten daher als Ergebnis:

Inhalt - Zurück - Weiter: Lösung von Problemen