14. Kegelschnitte als Hilfsmittel zur Lösung von Problemen

14.1. Die Lösung von kubischen Gleichungen

Wie bereits erwähnt, entdeckte Menaichmos die Kegelschnitte, als er das Problem der Verdopplung des Würfels zu lösen versuchte - eine mit Zirkel und Lineal nicht lösbare Aufgabe. Das ist gleichbedeutend mit der Lösung der kubischen Gleichung x³ = 2. Die Lösung kann man erhalten, indem man die Parabel y = x² mit der Hyperbel xy = 2 schneidet (siehe hier). Statt der Hyperbel kann man auch die Parabel y² = 2x verwenden.

Archimedes stellt sich im 2. Teil seiner Schrift "Über Kugel und Zylinder" die Aufgabe, eine Kugel mit dem Radius r so zu teilen, dass Volumina der beiden Segmente in einem gegebenen Verhältnis p:q stehen. Er kommt dabei auf eine Beziehung, die in heutiger Schreibweise lautet

(a - x) : c = b² : x²       bzw.

x²(a - x) = b²c

Dabei ist x die Höhe des einen Segments, a = 3r, b = 2r und c = pr/(p+q).

Archimedes gibt nicht an, wie er diese kubische Gleichung löst (oder dieser Teil der Schrift ist verlorengegangen). Aber nach Eutokius, einem Kommentator aus dem 6. Jahrhundert, hat er die Lösung mit Hilfe von Kegelschnitten gefunden:

Setzt man die linke Seite der obigen Proportion gleich e/y, erhält man (a - x)y = ce, die Gleichung einer Hyperbel; für die rechte Seite ergibt sich b²y = ex², die Gleichung einer Parabel. (e ist dabei eine beliebige Konstante.) Diese beiden Kurven haben einen Schnittpunkt, dessen x-Koordinate zwischen 0 und b liegt - das ist die gesuchte Höhe.

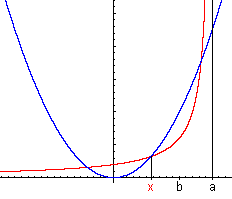
Eine systematische Untersuchung der kubischen Gleichungen findet sich erst beim persischen Mathematiker und Dichter Umar al-Hayyam (1048 - 1131). Da man damals noch nicht mit negativen Zahlen rechnete, musste er dabei 14 Gleichungstypen unterscheiden (siehe hier). Er fand zwar keine algebraische Lösung (das gelang erst Cardano im 16. Jahrhundert), aber er gibt zu jedem Typ an, wie man ihn mit Kegelschnitten lösen kann.

Eine Gleichung von der Form

x³ + ax² + bx = c

formt er beispielsweise um zu

x³ + ax² + p²x = p²q ;

die Lösung findet er durch den Schnitt der Hyperbel xy = pq mit dem Kreis über dem Durchmesser AB: A(-a/p), B(q/p).

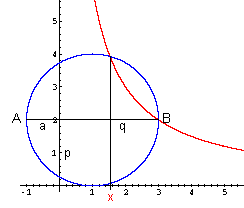
Hier die Lösung der Gleichung x³ + x² + 4x = 12.

René Descartes (1596 - 1650) fand eine Möglichkeit zur graphischen Lösung von Gleichungen 3. und 4. Grades. Dafür braucht man außer Zirkel und Lineal nur eine feste Parabel. (Man kann dann z.B. alle anderen Linien auf durchscheinendes Papier zeichnen und die Parabel mehrmals verwenden.)

Jede Gleichung 4. Grades kann durch eine Substitution auf die Form

x⁴ = px² + qx + r (*)

gebracht werden. Die Parabel hat die Gleichung

y = x²

Das setzt man in (*) ein:

y² = py + qx + r

Wenn man auf der linken Seite x² - y (= 0) addiert und umformt, erhält man

Das ist die Gleichung eines Kreises mit dem Mittelpunkt 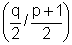. Die Abszissen der Schnittpunkte von Kreis und Parabel sind die Lösungen der Gleichung.

Eine Gleichung 3. Grades wird auf die Form (*) gebracht, indem man sie mit x multipliziert. Dabei ist r = 0, und der Kreis geht durch den Scheitel der Parabel. Die anderen Schnittpunkte ergeben die Lösungen der kubischen Gleichung.

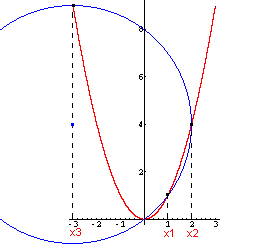
So löst Descartes die Gleichung x³ = 7x - 6.

14.2. Die Dreiteilung des Winkels

Auch die Aufgabe, einen beliebigen Winkel in drei gleiche Teile zu teilen, kann bekanntlich nicht mit Zirkel und Lineal gelöst werden. Pappos fand eine Lösung mit Hilfe einer Hyperbel:

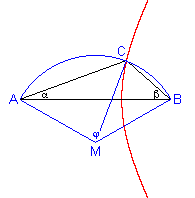
Angenommen, der Winkel φ bzw. der Kreisbogen AB wird durch den Punkt C gedrittelt. Wir betrachten jetzt das Dreieck ABC. Wegen des Peripheriewinkelsatzes ist <)AMC = 2β, <)BMC = 2α, also β = 2α. Pappos stellt fest, dass dann der Punkt C auf einer Hyperbel liegen muss. Genauer gesagt, ist a = AB/3, e = 2·AB/3 und B ein Brennpunkt der Hyperbel. Man kann also den Punkt C finden, indem man den gegebenen Kreisbogen mit der Hyperbel schneidet.

Eine weitere Lösung stammt von René Descartes. Sie besteht im Wesentlichen darin, dass man die Gleichung x³ = 3x - s auf die oben angegebene Art löst. Dabei ist s die Sehne des gegebenen Winkels im Einheitskreis und x die Sehne des gedrittelten Winkels.

Inhalt - Zurück - Weiter: Ort zu vier Geraden