Die Verdopplung des Würfels

a : x = x : y = y : b

Setzt man b = 2a, so ist x = a·³Ö2.

Während eine mittlere Proportionale leicht konstruiert werden kann (siehe "Mittelwerte": Geometrisches Mittel), ist die Konstruktion von zwei mittleren Proportionalen mit Zirkel und Lineal nicht möglich.

Die Entdeckung der Kegelschnitte

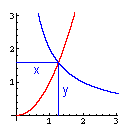Auf der Suche nach einer Lösung dieses Problems entdeckte Menaichmos (380 - 320 v. Chr.) die Kurven, die heute als Parabel und Hyperbel bekannt sind. Denn aus a : x = x : y erhält man x² = ay, die Gleichung einer Parabel, und aus a : x = y : b folgt xy = ab, die Gleichung einer Hyperbel. Die Koordinaten des Schnittpunktes dieser zwei Kurven sind daher die gesuchten Strecken x und y. Setzt man a = 1 und b = 2, ist x = ³Ö2.

Neusis-Konstruktionen

Nikomedes (280 - 210 v. Chr.) fand eine weitere Möglichkeit, zwei mittlere Proportionalen zu konstruieren. Im Fall von a = 1, b = 2 vereinfacht sich die ziemlich komplizierte Zeichnung zu folgender Konstruktion:

Wir gehen aus von einem Rechteck ABCD mit den Seitenlängen AD = 1, AB = Ö3 (und folglich der Diagonale AC = 2). Auf einem Lineal wird die Strecke EF = 1 markiert. Jetzt müssen wir das Lineal so an B anlegen, dass E auf der Verlängerung der Seite AB und F auf der Verlängerung der Diagonale zu liegen kommt. Dann ist BE = ³Ö2.

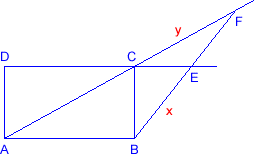
Beweis:
Der Winkel BCF ist 120°, also erhalten wir aus dem Cosinussatz:
BF² = BC² + CF² - 2·BC·CF·cos 120° Þ (x + 1)² = y² + y + 1
Aus dem Strahlensatz folgt
BE : EF = AC : CF Þ x : 1 = 2 : y Þ y = 2/x
Setzen wir das in die obere Gleichung ein und formen um, so ergibt sich
x³(x + 2) = 2(x + 2)
Da x nicht negativ sein kann, dürfen wir beide Seiten durch (x + 2) dividieren und erhalten x = ³Ö2, was zu beweisen war.

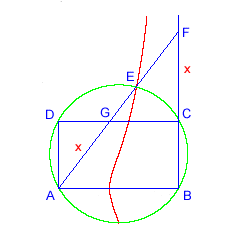
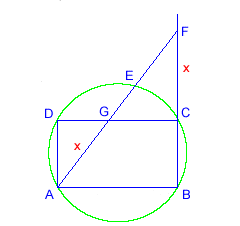Eine ähnliche Konstruktion erhält man, wenn man den Umkreis des Rechtecks zeichnet. Diesmal soll das Lineal durch A gehen, der Punkt E auf dem Kreis und der Punkt F auf der Verlängerung der Seite BC liegen. Der Beweis wird ähnlich wie vorhin geführt. (Angeblich stammt diese Konstruktion von Archimedes, ich konnte sie aber dort nirgends finden.)

Die Griechen nannten solche Konstruktionen "Neusis" (von neuein, sich neigen). Sie sind keine exakten Konstruktionen im euklidischen Sinn, weil man erst herumprobieren muss, bis man die richtige Stellung des Lineals gefunden hat.

Die Geradenkonchoide

Um solche Neusis-Konstruktionen einfacher durchführen zu können, erfand Nikomedes eine spezielle Kurve, die Konchoide (Muschelkurve). Sie wird folgendermaßen konstruiert:

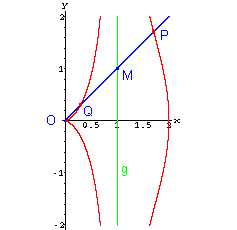
Wir gehen aus von einem Punkt O, dem Pol, und einer Geraden g, der Leitlinie. Eine beliebige Gerade durch O schneidet g im Punkt M. Die Punkte P und Q haben von M den konstanten Abstand k. Wenn sich die Gerade um O dreht, beschreiben P und Q die beiden Äste der Konchoide.

Wenn der Pol der Koordinatenursprung und die Gerade x = a die Leitlinie ist, lautet die Gleichung dieser Kurve in Polarkoordinaten

und in kartesischen Koordinaten

(x - a)²(x² + y²) = k²x².

Um die Muschelkurve zu zeichnen, verwendete man eigene Konchoidenzirkel - hier ein Modell aus dem "Laboratorio di matematica" der Universität von Modena:

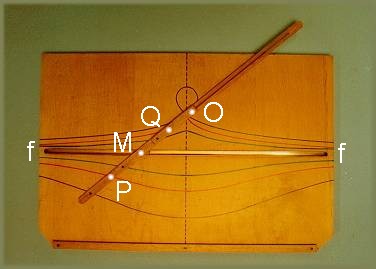
Die Konstruktion von Nikomedes kann jetzt durchgeführt werden, indem man eine Konchoide mit k = 1, B als Pol und CD als Leitlinie zeichnet:

Die andere Konstruktion geht ganz analog - diesmal nehmen wir A als Pol, BC als Leitlinie und verwenden den linken Ast der Kurve.

Die Kreiskonchoide

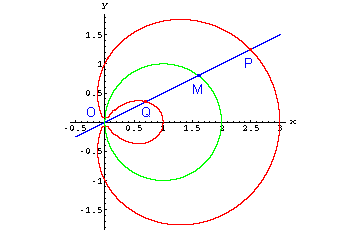Verwendet man als Leitlinie statt einer Geraden einen Kreis mit dem Durchmesser a, der durch den Pol geht, so erhält man eine Kreiskonchoide (auch Pascal'sche Schnecke genannt - nach Etienne Pascal, dem Vater von Blaise Pascal).

Die Gleichung lautet

r = a cos j + k       bzw.

(x² + y² - ax)² = k²(x² + y²)

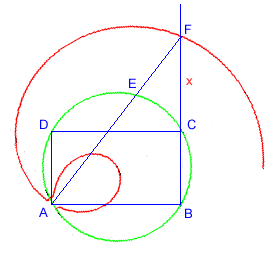
Die zweite Konstruktion zur Würfelverdopplung kann man auch mit einer Kreiskonchoide durchführen.

Weiter: Die Dreiteilung des Winkels