Die Dreiteilung des Winkels

Es ist sehr leicht, eine Strecke mit Hilfe des Strahlensatzes in drei gleiche Teile zu teilen (oder in eine beliebige andere Anzahl). Man kann auch einen Winkel mit Zirkel und Lineal halbieren. Aber eine Dreiteilung ist im allgemeinen nicht möglich (außer bei bestimmten Winkeln, z.B. 90°).

Hippokrates fand einen Weg, einen beliebigen Winkel mit Hilfe einer Neusis-Konstruktion zu dritteln:

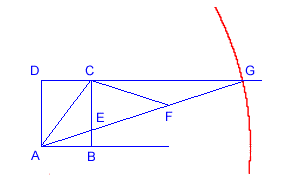Der Winkel a = BAC soll in drei gleiche Teile geteilt werden. Wir zeichnen das Rechteck ABCD und verlängern die Seite BC. Auf einem Lineal wird die Strecke EG = 2AC markiert. Es muss jetzt so an A angelegt werden, dass E auf BC und G auf der Verlängerung von CD liegt. (Das erreichen wir mit einer Konchoide mit A als Pol, BC als Leitlinie und k = 2BC.) Dann ist der Winkel b = BAE gleich a/3.

Beweis:
F sei der Mittelpunkt von EG. Weil BCG ein rechter Winkel ist, sind die Strecken EF, CF und FG alle gleich AC. CFG ist daher ein gleichschenkeliges Dreieck, und < FCG = < FGC = b.
< CFE ist also 2b, und da das Dreieck AFC ebenfalls gleichschenkelig ist, ist auch < EAC = 2b. Wir erhalten also: a = 3b, was zu beweisen war.

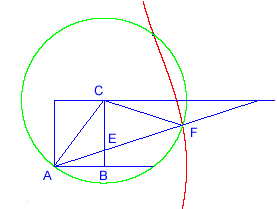
Eine andere Möglichkeit besteht darin, um C einen Kreis mit dem Radius AC zu zeichnen und das Lineal so durch A zu legen, dass die Strecke EF = AC zwischen BC und den Kreis zu liegen kommt. Auch das kann mit einer Konchoide konstruiert werden.

Eine sehr elegante Version dieser Konstruktion findet sich in Archimedes' "Buch der Hilfssätze":

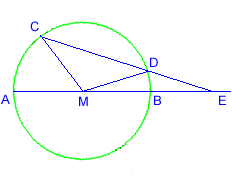
Der Winkel a = AMC soll gedrittelt werden. Wir legen das Lineal so durch den Punkt C, dass D auf dem Kreis und E auf der Verlängerung des Durchmessers liegt, wobei DE gleich dem Kreisradius ist. Dann ist < BMD = a/3.

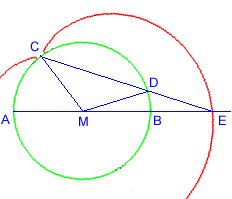
Diese Konstruktion kann man auch mit Hilfe einer Kreiskonchoide durchführen.

Andere Möglichkeiten

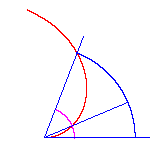
Mit Hilfe einer archimedischen Spirale kann ein Winkel in eine beliebige Anzahl von Teilen geteilt werden. Man nimmt einfach den Scheitel des Winkels als Mittelpunkt der Spirale und teilt den entsprechenden Radius.

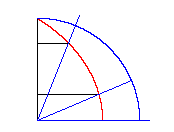
Auch mit einer Quadratrix ist die Winkelteilung leicht (eigentlich hat Hippias sie zu diesem Zweck erfunden): wir teilen die entsprechende Höhe im gewünschten Verhältnis.

Abschließende Bemerkungen

Wie erwähnt, konnte erst im 19. Jahrhundert mit den Mittel der modernen Algebra (Galois-Theorie) bewiesen werden, dass die drei klasischen Probleme mit Zirkel und Lineal unlösbar sind. Denn ein Punkt kann nur dann mit einer "euklidischen" Konstruktion gefunden werden, wenn seine Koordinaten die Lösungen von linearen oder quadratischen Gleichungen sind (eventuell muss man mehrere Gleichungen nacheinander lösen). Aber die Verdopplung des Würfels entspricht der Lösung der Gleichung

x³ = 2

Das ist eine Gleichung 3. Grades, die nicht auf eine quadratische Gleichung reduziert werden kann.

Auch die Dreiteilung des Winkels führt auf eine Gleichung 3. Grades. Denn wenn man den Winkel b = a/3 finden kann, kann man auch den Punkt mit den Koordinaten (cos b/sin b) konstruieren. Es gelten aber die Formeln

sin (3b) = 3 sin b - 4 sin³ b
cos (3b) = 4 cos³ b - 3 cos b

4x³ - 3x = a

lösen, die im Allgemeinen auch nicht auf eine quadratische Gleichung reduziert werden kann.

Die Zahl p schließlich ist transzendent, wie Lindemann 1882 bewiesen hat. Das heißt, sie kann überhaupt nicht die Lösung einer algebraischen Gleichung sein.

Doch diese Probleme haben die Mathematiker aller Zeiten zu vielen neuen Entdeckungen angeregt. Sie haben also für die Entwicklung der Mathematik eine bedeutende Rolle gespielt.

Literatur und Links

Archimedes, Abhandlungen. Übers. v. A. Czwalina-Allenstein, hrsg. v. W. Trageser, Frankfurt/Main 1996 (Reprint) (Ostwalds Klassiker der exakten Wissenschaften, Bd. 201)

Kaiser, Hans / Nöbauer, Wilfried: Geschichte der Mathematik für den Schulunterricht. Wien ²1998

Conway, John H. / Guy, Richard K.: Zahlenzauber. Von natürlichen, imaginären und anderen Zahlen. Basel 1997

The MacTutor History of Mathematics archive, Ancient Greek mathematics:
http://www-history.mcs.st-and.ac.uk/~history/Indexes/Greeks.html

Famous Curves Index:
http://www-history.mcs.st-and.ac.uk/~history/Curves/Curves.html

Algebraische Kurven:
http://www.fh-lueneburg.de/u1/gym03/expo/jonatur/wissen/mathe/kurven/kurven.htm