Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |

Wie wir gesehen haben, konnte man quadratische Gleichungen schon in der Antike lösen. Die Lösung der kubischen Gleichung (Gleichung 3. Grades) gelang aber erst den italienischen Algebraikern der Renaissancezeit. Sie wurde 1545 von Girolamo Cardano in seinem Hauptwerk "Ars magna" veröffentlicht.
Obwohl Cardano auch schon negative Lösungen untersucht, lässt er bei den Gleichungen nur positive Koeffizienten zu. Daher muss er - außer den trivialen Fällen und den von Al-Khwarizmi gelösten Gleichungen - 13 Typen von kubischen Gleichungen untersuchen:
x³ + ax = b "Ein Kubus und Unbekannte sind gleich einer Zahl" x³ = ax + b "Ein Kubus ist gleich Unbekannten und einer Zahl" x³ + b = ax "Ein Kubus und eine Zahl sind gleich Unbekannten" x³ = cx² + b "Ein Kubus ist gleich Quadraten und einer Zahl" x³ + cx² = b "Ein Kubus und Quadrate sind gleich einer Zahl" x³ + b = cx² "Ein Kubus und eine Zahl sind gleich Quadraten" x³ + cx² + ax = b "Ein Kubus, Quadrate und Unbekannte sind gleich einer Zahl" x³ + ax = cx² + b "Ein Kubus und Unbekannte gleich Quadraten und einer Zahl" x³ + cx² = ax + b "Ein Kubus und Quadrate gleich Unbekannten und einer Zahl" x³ = cx² + ax + b "Ein Kubus ist gleich Quadraten, Unbekannten und einer Zahl" x³ + b = cx² + ax "Ein Kubus und eine Zahl gleich Quadraten und Unbekannten" x³ + ax + b = cx² "Ein Kubus, Unbekannte und einen Zahl sind gleich Quadraten" x³ + cx² + b = ax "Ein Kubus, Quadrate und eine Zahl sind gleich Unbekannten"
Die Lösungsmethode für den ersten Fall wurde (unabhängig voneinander?) von Scipione Ferro und Niccolo Tartaglia gefunden. Dieser teilte sie Cardano mit, allerdings ohne Beweis. Cardano veröffentlichte die Lösung mit seinem eigenen Beweis, was zu einem heftigen Streit führte.
Ein Kubus und Unbekannte sind gleich einer Zahl
Im Kapitel XI der "Ars magna" löst Cardano eine Gleichung der Form x³ + ax = b folgendermaßen:
Er stellt die Unbekannte als Differenz zweier Hilfsvariablen dar - nennen wir sie u und v. Dann beweist er die Beziehung
(u-v)³ + 3uv(u-v) = u³ - v³,
indem er die Zerlegung eines Würfels betrachtet:
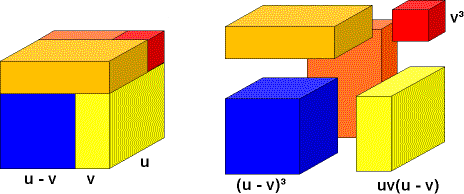
(Natürlich verwendet Cardano keine Formeln, sondern formuliert diesen Zusammenhang verbal.)
Wenn es also gelingt, u und v so zu bestimmen, dass
3uv = a und u³ - v³ = b,
ist das Problem gelöst.
Das können wir auch so formulieren:
Gesucht sind zwei Zahlen (nämlich u³ und v³), deren Produkt gleich (a/3)³ und deren Differenz
gleich b ist.
Damit haben wir aber eine Gleichung vom Typ B! Da Cardano seinen Euklid gut studiert hat,
kann er diese Gleichung lösen. Dann muss er nur noch die Kubikwurzeln aus den Lösungen ziehen
und voneinander subtrahieren.
Er formuliert daher folgende
REGEL Erhebe ein Drittel des Koeffizienten von x zur dritten Potenz; addiere dazu das Quadrat der halben Konstanten und ziehe daraus die Quadratwurzel. Diese schreibst du zweimal an, und zu einer addierst du die Hälfte der Zahl, die du quadriert hast, und von der anderen subtrahierst du diese Hälfte. Du hast dann ein Binomium und sein Apotome. Dann subtrahierst du die Kubikwurzel des Apotome von der Kubikwurzel des Binomium, und was übrigbleibt, ist der Wert von x.
(Auch die Ausdrücke "Binomium" und "Apotome" hat Cardano von Euklid übernommen.)
In heutiger Schreibweise lautet diese Formel:
x³ + ax = b
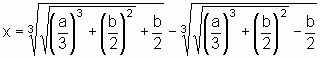
Im Anschluss an die Regel bringt Cardano noch einige Beispiele, z.B.:
x³ + 6x = 20 Erhebe 2, ein Drittel von 6, zur dritten Potenz, das ergibt 8; quadriere 10, die halbe Konstante; das ergibt 100. Addiere 100 und 8, das ist 108, und die Quadratwurzel ist Ö108. Das schreibst du zweimal an: zu einem addiere 10, die halbe Konstante, und von dem anderen subtrahiere es. Du erhältst also das Binomium Ö108 + 10 und das Apotome Ö108 - 10. Ziehe die Kubikwurzel aus diesen. Subtrahiere die Kubikwurzel des Apotome von der des Binomium, und du hast den Wert von x:
(Wie man mit dem Taschenrechner leicht überprüfen kann, ist x = 2.)
Ein Kubus ist gleich Unbekannten und einer Zahl
Im nächsten Kapitel, XII, behandelt Cardano Gleichungen der Form x³ = ax + b.
Diesen Fall löst er ganz analog zum vorigen:
Er stellt x als Summe zweier Hilfsvariablen u und v dar, so dass
3uv = a und u³ + v³ = b.
Damit hat er eine Gleichung vom Typ A und erhält folgende Lösungsregel:
REGEL Wenn der Kubus von einem Drittel des Koeffizienten von x nicht größer ist als das Quadrat der halben Konstanten, subtrahiere den ersteren vom letzteren; addiere die Quadratwurzel des Restes zur Hälfte der Konstanten und subtrahiere sie andrerseits von derselben Hälfte; wie oben erwähnt, hast du ein Binomium und ein Apotome. Die Summe ihrer Kubikwurzeln ergibt der Wert von x.
In heutiger Schreibweise lautet die Lösungsformel:
x³ = ax + b
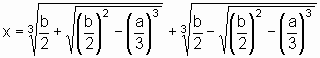
In den weiteren Kapiteln der "Ars magna" zeigt Cardano, wie man alle anderen Gleichungstypen durch ausgeklügelte Umformungen (wir würden sagen, Substitutionen) auf einen dieser beiden Fälle zurückführt. Er stellt auch eine von seinem Schüler Ludovico Ferrari entdeckte Methode vor, mit der man sogar Gleichungen 4. Grades auf derselben Grundlage lösen kann.
Wie bereits erwähnt, weiß Cardano auch schon, dass eine Gleichung auch negative Lösungen haben kann (er nennt sie "fiktive" oder "falsche" Lösungen). Im ersten Kapitel untersucht er, wieviele Lösungen bei den verschiedenen Gleichungstypen auftreten können. Er erwähnt zum Beispiel, dass eine positive Lösung der Gleichung x³ = ax + b einer negativen Lösung der Gleichung x³ + b = ax entspricht. Trotzdem versucht er negative Lösungen, so gut es geht, zu vermeiden. So gibt er in Kapitel XIII einen ziemlich komplizierten Lösungsweg für den Fall "Ein Kubus und eine Zahl sind gleich Unbekannten" an, obwohl er diese Gleichung mit der vorhin erwähnten Regel ganz leicht lösen könnte.
In Kapitel XXXVII deutet Cardano sogar schon das Rechnen mit komplexen Zahlen an - aber man merkt genau, wieviel Bauchweh ihm der Gedanke noch bereitet!
Mit der Erfindung der algebraischen Schreibweise durch Vieta und Descartes wurde das Lösen von Gleichungen wesentlich einfacher. Langsam wurde es üblich, auch negative Zahlen und 0 als Koeffizienten zuzulassen. Daher müssen wir heute nur mehr eine Lösungsformel für quadratische Gleichungen lernen. Doch ohne die Vorarbeiten von Euklid, Al-Khwarizmi, Cardano und vielen anderen wäre das wohl nicht möglich geworden.
Euklid: Die Elemente. Übers. u. hrsg. v. Clemens Thaer, Frankfurt/Main 31997 (Reprint) (Ostwalds Klassiker der exakten Wissenschaften, Bd. 235)
Al-Khwarizmi: The Algebra of Mohammed Ben Musa. Transl. and ed. by Frederic Rosen, Olms, Hildesheim, 1986 (engl.)
Cardano, Girolamo: Ars Magna or The Rules of Algebra. Transl. and ed. by. T. Richard Witmer, New York 1968 (engl.)
Kaiser, Hans / Nöbauer, Wilfried: Geschichte der Mathematik für den Schulunterricht. Wien 21998
"Alt und chic" (Babylonische Lösungsmethode für quadratische Gleichungen):
http://www.educeth.ch/lehrpersonen/mathematik/unterrichtsmaterialien_mat/arithmetik_algebra/quadr_gleich/quadgl.pdf, S. 37
Old Babylonian 'Quadratic' Problems (engl.):
http://it.stlawu.edu/~dmelvill/mesomath/Rectangular.html
An Overview of Babylonian Mathematics (engl.):
http://www-history.mcs.st-and.ac.uk/~history/HistTopics/Babylonian_mathematics.html
Euclid's Elements, kommentiert von D. E. Joyce (engl.):
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
Kaske, Rainer: Quadratische Gleichungen bei al-Khwarizmi:
http://www.raikas.net/alkh1.html