Home

Ich über mich

Texte

Religion

Mathematik

Spiele

Gästebuch

Quadratische Gleichungen bei Al-Khwarizmi

Muhammad Ibn Musa al-Khwarizmi (ca. 780 - 850) war der einer der bedeutendensten arabischen Mathematiker. Unter anderem hat er das Rechnen mit dem indischen Stellenwertsystem in der arabischen Mathematik eingeführt. Bekanntlich haben die Europäer dieses System später als "arabische Ziffern" übernommen. Daher ist Al-Khwarizmis Name in der lateinischen Form "Algorithmus" zur allgemeinen Bezeichnung für Rechenverfahren geworden. Vom Titel seines Buchs "Hisab al-gabr w'al muqabala" (Über die Rechenverfahren durch Ergänzen und Ausgleichen) leitet sich unser Wort "Algebra" her.

Al-Khwarizmi löst Gleichungen mit den Methoden, die wir heute noch verwenden: Abziehen von gleichen Ausdrücke auf beiden Seiten der Gleichung ("Ausgleichen"), um gleiche Potenzen zusammenzufassen, und Hinüberschaffen eines negativen Gliedes auf die andere Seite ("Ergänzen"), sodass sich positive Koeffizienten ergeben (negative Zahlen wurden ja noch nicht verwendet).
Allerdings kennt er noch keine algebraische Schreibweise, sondern gibt - wie Euklid - für alle Rechenregeln verbale Erklärungen.

Weil Al-Khwarizmi nur positive Koeffizienten zulässt, unterscheidet er sechs Grundtypen von Gleichungen:

x² = bx	"Quadrate sind gleich Wurzeln"
x² = b	"Quadrate sind gleich Zahlen"
ax = b	"Wurzeln sind gleich Zahlen"
x² + ax = b	"Quadrate und Wurzeln sind gleich Zahlen"
x² + b = ax	"Quadrate und Zahlen sind gleich Wurzeln"
ax + b = x²	"Wurzeln und Zahlen sind gleich Quadraten"

(Mit "Wurzel" ist immer die Unbekannte x gemeint.)
Für jeden dieser Typen gibt er eine Lösungsregel an, die er dann geometrisch begründet.

Wir werden jetzt sehen, wie Al-Khwarizmi gemischtquadratische Gleichungen (die letzten drei Gleichungstypen) löst.

Quadrate und Wurzeln sind gleich Zahlen

"Ein Quadrat und 10 Wurzeln ergeben 39 Einheiten;" das heißt, wie groß muss das Quadrat sein, welches, wenn es um 10 seiner eigenen Wurzeln ergänzt wird, 39 ergibt? Die Lösung ist dies: du halbierst die Anzahl der Wurzeln, was in dem vorliegenden Beispiel 5 liefert. Dies multiplizierst du mit sich selbst; das Produkt ist 25. Addiere dies zu 39; die Summe ist 64. Nun nimm die Wurzel von diesem, welche 8 ist, und subtrahiere davon die Hälfte der Anzahl der Wurzeln, was 5 ist; der Rest ist 3. Dies ist die Wurzel des Quadrats, nach welcher du gesucht hast; das Quadrat selbst ist 9.

Wie kommt Al-Khwarizmi zu dieser Lösung? Vielleicht hat er die Gleichung folgendermaßen umgeformt:

x² + 10x = 39
x(x + 10) = 39

Das ist eine Gleichung vom Typ B, wobei die kleinere Zahl gesucht wird. Der Lösungsweg und die "Formel", die sich dabei ergibt, entsprechen genau der Konstruktion von Euklid.

Al-Khwarizmi gibt aber noch eine andere geometrische Begründung:

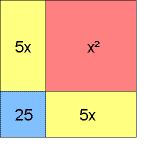
Er geht aus von einem Quadrat mit der (unbekannten) Seite x. Daran fügt er zwei Rechtecke mit der Breite 5, die also zusammen den Flächeninhalt 10x haben. Die Gesamtfläche beträgt also laut Angabe 39 Einheiten. Jetzt ergänzt er diese Figur zu einem Quadrat. Das kleine Quadrat hat den Flächeninhalt 5² = 25, die Fläche des ganzen Quadrats beträgt daher 39 + 25 = 64. Die Seitenlänge ist Ö64 = 8, daher ist x = 8 - 5 = 3.

Al-Khwarizmis geometrischer "Beweis" ist viel anschaulicher als der von Euklid. Er entspricht der Methode der "quadratischen Ergänzung", mit der wir heute noch quadratische Gleichungen lösen. Allerdings ist er nicht konstruktiv: er gibt nicht an, wie die gesuchte Strecke konstruiert werden kann, sondern bietet "nur" eine nachträgliche Begründung für eine Rechenregel.

Die anderen beiden Fälle werden folgendermaßen gelöst:

Wurzeln und Zahlen sind gleich Quadraten

"3 Wurzeln und 4 einfache Zahlen sind gleich einem Quadrat." Lösung: Halbiere die Wurzeln; die Hälfte ist 1½. Multipliziere dies mit sich selbst; das Produkt ist 2¼. Addiere dies zu der 4; die Summe ist 6¼. Ziehe die Wurzel; es sind 2½. Addiere dies zu der Hälfte der Wurzeln, welche 1½ war; die Summe ist 4. Dies ist die Wurzel des Quadrats, und das Quadrat ist 16.

Diese Gleichung können wir so umformen:

x² = 3x + 4
x² - 3x = 4
x(x - 3) = 4

Das ergibt wieder eine Gleichung vom Typ B; diesmal wird die größere Zahl gesucht. Auch hier entspricht der Lösungsweg genau der euklidischen Konstruktion.

Quadrate und Zahlen sind gleich Wurzeln

"Ein Quadrat und 21 Zahlen sind gleich 10 Wurzeln." Das heißt, was muss das Quadrat sein, welches, wenn 21 Einheiten zu ihm addiert werden, gleich wird zu 10 Wurzeln desselben Quadrats. Lösung: Halbiere die Anzahl der Wurzeln; die Hälfte ist 5. Multipliziere dies mit sich selbst; das Produkt ist 25. Subtrahiere davon die 21 Zahlen (...), der Rest ist 4. Ziehe daraus die Wurzel, das ist 2. Subtrahiere dies von der Hälfte der Wurzeln, was 5 ist; der Rest ist 3. Dies ist die Wurzel des Quadrats, welche du gesucht hast; und das Quadrat ist 9. Oder: Addiere die Wurzel zu der Hälfte der Wurzeln; die Summe ist 7; dies ist die Wurzel des Quadrats, nach welcher du gesucht hast, und das Quadrat selbst ist 49.
Wenn du auf solch einen Fall triffst, versuche die Lösung durch Addition, und falls das nicht hilft, dann wird es sicherlich die Subtraktion. Denn in diesem Fall können sowohl Addition als auch Subtraktion benutzt werden, was in den anderen Fällen (...) nicht möglich ist.
Und beachte: Falls bei einer Aufgabe, die zu diesem Fall gehört, das Produkt der Hälfte der Anzahl der Wurzeln mit sich selbst weniger ist als die Zahlen, dann ist diese Aufgabe unmöglich. Aber: Wenn das Produkt gleich den Zahlen ist, dann ist die Wurzel des Quadrats gleich der Hälfte der Anzahl der Wurzeln, ohne Addition oder Subtraktion.

Diese Gleichung ergibt in unserer Schreibweise:

10x = x² + 21
10x - x² = 21
x(10 - x) = 21

Das ist eine Gleichung vom Typ A - dabei gibt es zwei positive Lösungen. Deswegen gibt Al-Khwarizmi auch bei diesem Typ als einzigem zwei Lösungen an und weist auch auf die Möglichkeit hin, dass es keine Lösung gibt (wenn der Ausdruck, aus dem die Wurzel gezogen werden soll, negativ wird - diese Möglichkeit musste ja auch Euklid ausschließen.)

zurück - nach oben - weiter