Home

Ich über mich

Texte

Religion

Mathematik

Spiele

Gästebuch

Gleichungen bei Euklid

Euklid lebte um 300 v.Chr. in Alexandria. In seinem Hauptwerk, den "Elementen", hat er das gesamte mathematische Wissen der damaligen Zeit zusammengestellt. Dabei stand die Geometrie im Zentrum; auch algebraische Probleme wurden auf geometrischem Weg gelöst. Eine besondere Rolle spielte dabei die Theorie der Flächenanlegung, die auf die Pythagoreer zurückgeht.

In Buch I, § 44 behandelt Euklid die sogenannte "parabolische Flächenanlegung" (von paraballein, gleichkommen):

An eine gegebene Strecke ein einem gegebenes Dreieck gleiches Parallelogramm in einem gegebenen (...) Winkel anzulegen.

Betrachten wir den einfacheren Fall, dass es sich um ein Rechteck handelt, so besteht die Aufgabe darin, ein Rechteck mit gegebener Länge a und gegebenem Flächeninhalt b zu konstruieren. Das können wir auch als lineare Gleichung anschreiben:

a·x = b

Das Bild zeigt, wie es gemacht wird:

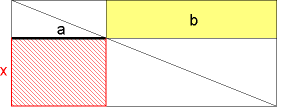
Da die Diagonale das große Rechteck in zwei gleichgroße Dreiecke teilt und auch die kleinen Dreiecke zu beiden Seiten der Diagonale gleich groß sind, müssen auch die Rechtecke b und a·x denselben Flächeninhalt haben.

In Buch I, § 14 löst Euklid die Aufgabe,

Ein einer gegebenen geradlinigen Figur gleiches Quadrat zu errichten.

Das entspricht einer quadratischen Gleichung:

x² = b

Wenn die gegebene Figur ein Rechteck ist, besteht die Aufgabe darin, das geometrische Mittel der Seitenlängen zu finden. Wie das geht, sieht man (mit etwas anderen Bezeichnungen) auf der Seite "Mittelwerte".

Für die Lösung von gemischtquadratischen Gleichungen benutzten die Griechen zwei andere Arten der Flächenanlegung.

Die "elliptische Flächenanlegung" (von elleipein, ermangeln) wird in Buch VI, § 28 erklärt:

An eine gegebene Strecke ein einer gegebenen geradlinigen Figur gleiches Parallelogramm so anzulegen, dass ein einem gegebenen ähnliches Parallelogramm fehlt; hierbei darf die gegebene geradlinige Figur nicht größer sein als das dem fehlenden ähnliche über der Hälfte der Strecke zu zeichnende Parallelogramm.

Wir betrachten wieder den einfacheren Fall, dass das gegebene Parallelogramm ein Quadrat ist (nur dieser Spezialfall wird später benutzt) - dann ist die gesuchte Figur ein Rechteck mit gegebenem Flächeninhalt b:

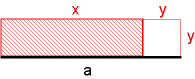
Es ist also ein Rechteck mit Flächeninhalt b gesucht, dessen Seiten x und y zusammen die Strecke a ergeben. Das entspricht einer Gleichung vom Typ A (die Summe und das Produkt zweier Zahlen sind bekannt). Wir können sie auch so schreiben:

x·(a - x) = b

Euklid löst diese Aufgabe folgendermaßen:

• Halbiere die Strecke a und zeichne das Quadrat über der Hälfte. Wenn die Fläche dieses Quadrats gleich b ist, bist du fertig.
• Andernfalls konstruiere ein Quadrat (blau), dessen Flächeninhalt gleich dem Quadrat über der halben Strecke, vermindert um b, ist. (Wie das geht, hat Euklid in VI, § 25 gezeigt.)
• Vervollständige die Figur.

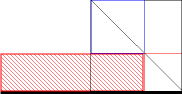
In heutiger Schreibweise ausgedrückt, lautet das Ergebnis:

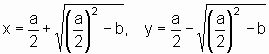
Der zweite Teil der Angabe stellt sicher, dass unter der Wurzel keine negative Zahl steht.

Der nächste Abschnitt (VI, § 29) behandelt die "hyperbolische Flächenanlegung" (von hyperballein, übertreffen):

An eine gegebene Strecke ein einer gegebenen geradlinigen Figur gleiches Parallelogramm so anzulegen, dass ein einem gegebenen ähnliches Parallelogramm überschießt.

Wir betrachten wieder den einfacheren Fall:

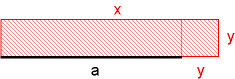
Es ist also ein Rechteck mit Flächeninhalt b gesucht, dessen Länge um a größer als die Breite ist. Das entspricht einer Gleichung vom Typ B (die Differenz und das Produkt zweier Zahlen sind bekannt). In heutiger Schreibweise lautet sie:

x·(x - a) = b
bzw.
y·(y + a) = b

Euklids Lösungsweg:

• Halbiere die Strecke a und zeichne das Quadrat über der Hälfte.
• Konstruiere ein Quadrat (blau), dessen Flächeninhalt gleich dem Quadrat über der halben Strecke, vermehrt um b, ist.
• Vervollständige die Figur.

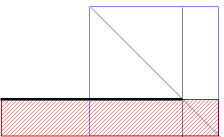
Das Ergebnis in heutiger Schreibweise:

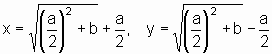
(Wem die Bezeichnungen der Flächenanlegungen bekannt vorkommen, der hat Recht: Apollonius von Perge hat später aus diesen Bezeichnungen die Namen der Kegelschnitte Ellipse, Parabel und Hyperbel abgeleitet.)

Im X. Buch der "Elemente" untersucht Euklid die verschiedenen Arten von irrationalen Zahlen, die beim Lösen quadratischer Gleichungen auftreten können. Er bezeichnet die Summe zweier Strecken, die kein rationales Verhältnis zueinander haben (z.B. Ö2 + 1), als Binomiale (X, § 36), die Differenz zweier solcher Strecken (z.B. Ö2 - 1) als Apotome (X, § 73). Diese Bezeichnungen wollen wir uns für später merken.

zurück - nach oben - weiter