Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Quadratische Gleichungen bei den Babyloniern
Gleichungen bei Euklid
Quadratische Gleichungen bei Al-Khwarizmi
Die Lösung der kubischen Gleichung durch Cardano
Literatur
Im Mathematikunterricht lernt man, wie man Gleichungen löst - zuerst lineare, später auch
quadratische und noch schwierigere Gleichungen. Wir sind dabei eine bestimmt Schreibweise
gewohnt (z.B.: 2x + 3 = 9) und benutzen bestimmte Umformungsregeln und Formeln.
Diese algebraische Schreibweise stammt aus dem 16. Jahrhundert. Auch der Gebrauch von negativen
Zahlen wurde erst um diese Zeit üblich. Doch davor gab es schon eine hochentwickelte
Mathematik. Wie haben die Mathematiker des Altertums und Mittelalters Gleichungen, speziell
quadratische Gleichungen gelöst?

In babylonischen Texten finden sich viele Aufgaben der Art:
Die Länge und Breite (eines Rechtecks) ergeben zusammen 50, die Fläche ist 600. Wie lang sind die Seiten?
In heutiger Schreibweise würden wir die Länge mit x und die Breite mit 50 - x bezeichnen und erhielten folgende Gleichung:
x (50 - x) = 600
50x - x² = 600
x² - 50x + 600 = 0
Diese Aufgabe führt also auf eine quadratische Gleichung.
Bevor wir uns ansehen, wie die Babylonier dieses Problem gelöst hätten, betrachten wir eine
einfachere Aufgabe:
Von zwei Zahlen sind die Summe und die Differenz bekannt. Wie groß sind die Zahlen?
Die Lösung lautet, wie man leicht nachrechnet:
Die eine Zahl ist die halbe Summe plus die halbe Differenz, die andere Zahl die halbe Summe
minus der halben Differenz.
In moderner Schreibweise:
x + y = S
x - y = D
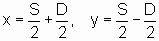
Die babylonischen Mathematiker schafften es nun, Probleme wie das zuerst genannte auf die
einfachere Aufgabe zurückzuführen. Sie kannten nämlich die Rechenregel:
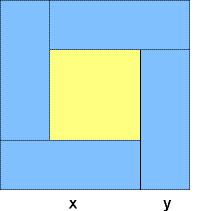
Das Quadrat der Summe zweier Zahlen ist gleich dem Quadrat der Differenz, vermehrt um das
vierfache Produkt.
Eine anschauliche Erklärung gibt die folgende Figur:
Damit können wir jetzt zwei Grundtypen von Gleichungen lösen:
A: Die Summe und das Produkt zweier Zahlen sind bekannt. Wie groß sind die Zahlen?
Wir berechnen das Quadrat der Summe und ziehen davon das vierfache Produkt ab. Aus dem Ergebnis
ziehen wir die Wurzel, um die Differenz zu erhalten. Die beiden Zahlen berechnen wir jetzt
nach dem vorigen Beispiel als (halbe Summe plus halbe Differenz) und (halbe Summe minus halbe
Differenz).
Wenn man die Wurzel noch etwas umformt, erhält man folgende Formeln:
x + y = S
x·y = P
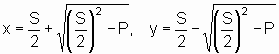
Das erinnert schon sehr an die heute übliche Lösungsformel für quadratische Gleichungen! Die Babylonier haben die Formel natürlich nicht so angeschrieben, sondern als verbale Rechenregel angegeben.
B: Die Differenz und das Produkt zweier Zahlen sind bekannt. Wie groß sind die Zahlen?
Wir berechnen das Quadrat der Differenz und addieren das vierfache Produkt. Aus dem Ergebnis
ziehen wir die Wurzel, um die Summe zu erhalten. Die beiden Zahlen können wir jetzt wieder
nach dem ersten Beispiel berechnen.
x - y = D
x·y = P
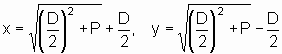
Das Beispiel aus der Einleitung gehört zum Typ A. Wir berechnen daher: Die halbe Summe ist 25, das Quadrat davon 625. Davon wird das Produkt abgezogen: 625 - 600 = 25, Wurzel aus 25 ist 5. Die Länge beträgt 25 + 5 = 30, die Breite 25 - 5 = 20.
Ein Beispiel für Typ B:
Die Fläche ist 60, die Länge übertrifft die Breite um 7.
Wir rechnen: Die halbe Differenz ist 3,5, das ergibt quadriert 12,25. Das Produkt wird addiert: 12,25 + 60 = 72,25, die Wurzel daraus ist 8,5. Die Länge beträgt 8,5 + 3,5 = 12, die Breite 8,5 - 3,5 = 5.
Auch kompliziertere Aufgaben wurden auf die Standardformen zurückgeführt und mit entsprechenden Rechenvorschriften gelöst:
Die Fläche und die Seite eines Quadrats habe ich addiert und ¾ ist es.
1, den Koeffizienten nimmst du. Die Hälfte von 1 brichst du ab, ½ und ½ multiplizierst du. ¼ zu ¾ fügst du hinzu. Und 1 hat 1 als Quadratwurzel. ½, das du mit sich selbst multipliziert hast, von 1 subtrahierst du, und ½ ist das Quadrat.
Für solche und ähnliche Berechnungen besaßen die babylonischen Gelehrten Multiplikations- und Wurzeltabellen (wie z.B. die Tafel auf der Abbildung oben: Plimpton 322, eine Tabelle von pythagoreischen Zahlentripeln).