Fixpunktiteration

Bei manchen Gleichungen ist es auch günstig, sie in die Form F(x) = x umzuformen. Man sucht dann den Fixpunkt der Funktion F, also den Schnittpunkt des Graphen mit der Geraden y = x. (Die Bezeichnung F(x) soll darauf aufmerksam machen, dass es hier um eine andere Funktion geht als in den vorigen Beispielen. Es handelt sich nicht um eine Stammfunktion.) Wir gehen wieder von einer Näherungslösung x₀ aus und setzen sie in die Funktion ein. Wenn wir Glück haben, liegt der Funktionswert F(x₀) näher beim Fixpunkt als der Ausgangswert. Dieses Ergebnis setzen wir wieder in die Funktion ein, bis wir mit dem Ergebnis zufrieden sind.

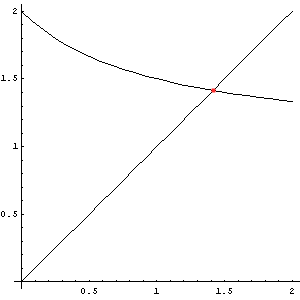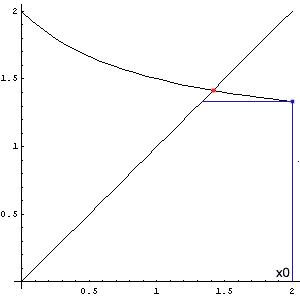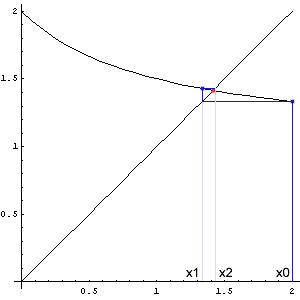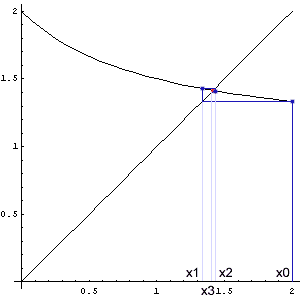
Wie man sieht, nähern sich die Werte nur dann der richtigen Lösung, wenn der Funktionsgraph dort nicht zu steil ist. Genauer gesagt, muss in einer Umgebung des Fixwertes gelten: |F'(x)| < 1. (Das zeigt man mit Hilfe des Zwischenwertsatzes der Differentialrechnung.) Je kleiner der Betrag der 1. Ableitung ist, umso schneller konvergiert das Verfahren. Es kommt also darauf an, die ursprüngliche Gleichung möglichst geschickt umzuformen.

Beispiel:

Wir gehen wieder aus von der Gleichung

x² - 2 = 0

und formen um:

x² + x = x + 2
x(x + 1) = (x + 1) + 1    | :(x + 1)

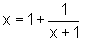
Wir suchen also den Fixwert der Funktion 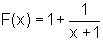(siehe Bild oben). Als Ausgangswert wählen wir x₀ = 2.

x0	x1 = F(x0)	x1² - 2
2	4/3 = 1,3333	-2/9 = -0,2222
4/3	10/7 = 1,4268	2/49 = 0,0408
10/7	24/17 = 1,4118	-2/289 = -0,0069
24/17	58/41 = 1,4146	2/1681 = 0,0012
58/41	140/99 = 1,4141	-2/9801 = -0,0002

In diesem Beispiel ist also die Fixpunktiteration nicht besser als die Regula falsi-Methode.

(Die naheliegende Umformung 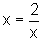hätte uns nicht weitergebracht, denn dann wäre F'(√(2)) = -1. Die Näherungswerte würden ständig zwischen x₀ und 2/x₀ hin und her springen.)

Anwendung: Planetenbahnen (Keplergleichung)

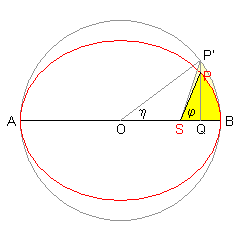
Die Erde durchläuft Anfang Jänner den sonnennächsten Punkt ihrer Bahn (Perihel). Um welchen Winkel, von der Sonne aus gesehen, hat sie sich 3 Monate später weiterbewegt? (Die Zeichnung zeigt die Situation zu einem anderen Zeitpunkt; S = Sonne, P = Planet = Erde.)

Um die Position eines Planeten zu einem bestimmten Zeitpunkt zu berechnen, braucht man die Keplergleichung:

μ = η - ε·sin(η)

ε ist die Exzentrizität der Bahnellipse. Bei der Erde beträgt sie ca. 1/60. μ, die "mittlere Anomalie" ist proportional zur verstrichenen Zeit. In unserem Beispiel ist das π/2, ein Viertel eines vollen Umlauf. η, die "exzentrische Anomalie", müssen wir berechnen. (Genauere Erklärungen im Artikel über Kegelschnitte.)

Wir formen die Gleichung um zu

η = μ + ε·sin(η)

und verwenden die Fixpunktmethode. Weil ε sehr klein ist, wird sich η nicht sehr von μ unterscheiden. Wir können daher π/2 als Anfangswert verwenden.

η0	η1
1,570796	1,587462
1,587462	1,587461

Wir haben also schon im ersten Rechenschritt 5 richtige Dezimalstellen erhalten! Das liegt daran, dass F'(x) sehr klein, nämlich kleiner als ε ist. Der Fehler wird also in jedem Schritt kleiner als 1/60 des vorigen.

berechnen. Wir erhalten φ = 1,6037 = 91,88°. Die Erde (bzw. von der Erde aus gesehen, die Sonne) hat sich also um 91,88° weiterbewegt.

Zurück

Links:

Nichtlineare Gleichungen (aus einem Skriptum über "Grundbegriffe der Numerik"): siehe die Abschnitte "Iterationsverfahren", "Bisektionsverfahren", "Newton-Verfahren", "Sekanten-Verfahren"

Animations for Root-Finding: viele anschauliche Animationen. Man sieht auch die Sonderfälle, bei denen das jeweilige Verfahren nicht zum Ziel führt. Unter "Module" kommt man zur zugehörigen Theorie. (englisch)

Wikipedia: Bisektion - Regula Falsi - Sekantenverfahren - Newton-Verfahren