Newtonsches Näherungsverfahren

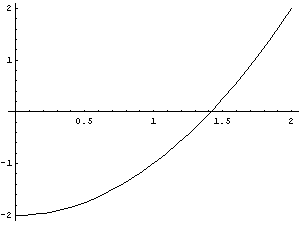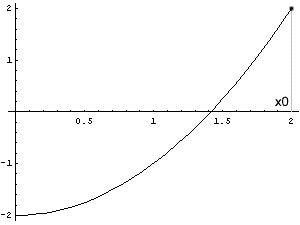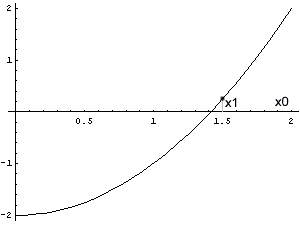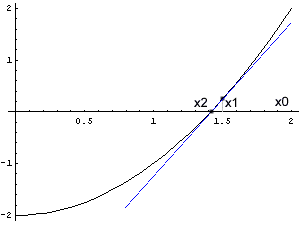
Beim Regula falsi- bzw. Sekantenverfahren haben wir den Funktionsgraphen durch eine Gerade ersetzt. Die beste lineare Näherung an eine Funktion in der Umgebung eines Punktes ist die Tangente in diesem Punkt. Beim Newton-Verfahren (auch als Newton-Raphson-Methode bekannt) geht man daher nur von einem Näherungswert aus, bestimmt die Tangente an dieser Stelle (wenn sie existiert) und berechnet ihre Nullstelle. Das wiederholt man wieder so lange, bis man mit der erreichten Genauigkeit zufrieden ist. (Man kann das Verfahren auch als Grenzfall des Sekantenverfahrens auffassen: die beiden Stützwerte fallen zusammen, und die Sekante wird durch die Tangente ersetzt.)

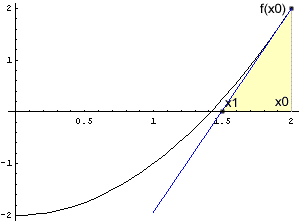
Aus dem gelben Dreieck können wir ablesen:

Das können wir umformen zur Formel

Beispiel:

Wir testen die Methode wieder an der Gleichung x² - 2 = 0 und verwenden den Anfangswert 2.

x0		f(x1)
2	3/2 = 1,5	1/4 = 0,25
3/2	17/12 = 1,4167	1/144 = 0,0069
17/12	577/408 = 1,4142	0,000006

Wie man sieht, konvergiert das Newton-Verfahren besonders schnell - nach 3 Schritten haben wir bereits 4 richtige Dezimalstellen, und bei jedem weiteren Schritt verdoppelt sich die Anzahl der Stellen. Man spricht dabei von "quadratischer Konvergenz". Das gilt aber nur, wenn die gesuchte Lösung eine einfache Nullstelle von f(x) ist. Bei mehrfachen Nullstellen ist die Konvergenzgeschwindigkeit nur linear.

Das Newtonsche Näherungsverfahren ist also eine sehr praktische Methode, um Gleichungen zu lösen. Man kann es aber nur anwenden, wenn die gegebene Funktion in der Nähe der Nullstelle nicht nur stetig, sondern auch differenzierbar ist. Und man kann auch hier Pech haben: Wenn man einen ungünstigen Startwert (mit sehr flacher Tangente) wählt, findet man entweder gar keine Nullstelle oder eine andere als die, die man gesucht hat.

Anwendung: Schaf auf kreisförmiger Wiese

Ein Schaf ist am Rand einer kreisförmigen Wiese angebunden. Wie lang muss die Leine sein, damit es genau die halbe Wiesenfläche abgrasen kann? (In den meisten Fassungen dieses Rätsels ist von einer Ziege die Rede, aber weil es auch ein anderes, sehr bekanntes "Ziegenproblem" gibt, habe ich mich für ein Schaf entschieden.)

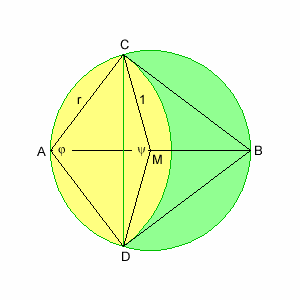
Die gesuchte Fläche ist der Durchschnitt zweier Kreise. Das Schaf ist im Punkt A angebunden. Der Einfachheit halber setzen wir den Radius der Wiese gleich 1. Wir müssen also den Radius des anderen Kreises so bestimmen, dass der Inhalt der Durchschnittsfläche π/2 beträgt. Diese Fläche besteht aus zwei Kreissegmenten und beträgt daher

(1)       A = r²/2·(φ - sin(φ)) + 1/2·(ψ - sin(ψ))

Aus dem rechtwinkeligen Dreieck ABC können wir ablesen

(2)       cos(φ/2) = r/2;

nach einer trigonometrischen Formel ist daher

(3)       r² = 4 cos²(φ/2) = 2(cos(φ) + 1).

Die Winkelsumme im gleichschenkeligen Dreieck AMC liefert uns

(4)       ψ/2 = π - φ,

also

(5)       sin(ψ) = 2sin(ψ/2)cos(ψ/2) = -2sin(φ)cos(φ).

Wenn wir (3), (4) und (5) in (1) einsetzen und umformen, ergibt sich für die Fläche

(6)       A = φ·cos(φ) - sin(φ) + π

Das soll gleich π/2 sein; wir müssen daher folgende Gleichung lösen:

φ·cos(φ) - sin(φ) + π/2 = 0

An der Skizze erkennt man, dass φ etwas kleiner als 120° sein muss. Wir wählen daher als Startwert für das Newton-Verfahren φ₀ = 2.

φ0	φ1	f(φ1)
2	1,9061	0,0007
1,9061	1,9057	~ 0

Der Winkel φ beträgt also 1,9057 = 109,2°, und aus (2) erhalten wir r = 1,1587.

Zurück - Weiter: Fixpunktiteration