Regula Falsi

Die "Regel des falschen Ansatzes" ist eine schon lange bekannte Methode zur Lösung von Gleichungen. Sie wurde zum Beispiel von Adam Ries gelehrt. Man geht dabei von zwei falschen Lösungen aus (daher der Name), um mit ihrer Hilfe die richtige zu finden. Allerdings liefert die Methode nur dann die genaue Lösung, wenn es sich um eine lineare Gleichung handelt. Sonst erhält man eine Näherungslösung.

Die selbe Idee steht auch hinter der linearen Interpolation. Als man Funktionswerte wie Logarithmus oder Sinus noch aus Tabellen ablesen musste, stand man oft vor dem Problem, Zwischenwerte zu finden, die nicht in der Tabelle standen. Dabei nahm man an, dass die Funktion zwischen den beiden Werten linear verläuft. Wenn man z. B. den Logarithmus von 2113 ermitteln musste, las man aus der Tabelle ab: log(2110) = 3,3243, log(2120) = 3,3263. Dann addierte man zum unteren Wert 3/10 der Differenz und erhielt log(2113) = 3,3243 + 0,3·0,0020 = 3,3249. Manche Logarithmentafeln hatten zur Vereinfachung neben den eigentlichen Tabellen noch "Proportionaltäfelchen", also Listen der Korrekturzahlen, die man addieren musste.

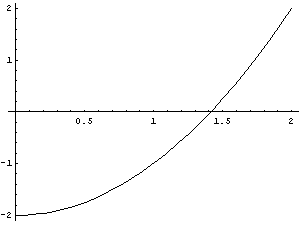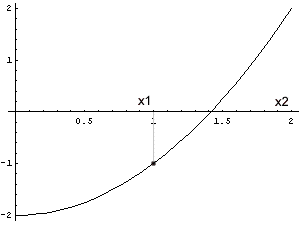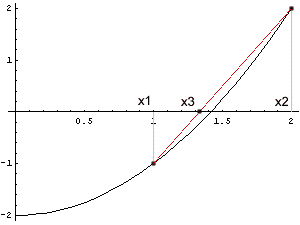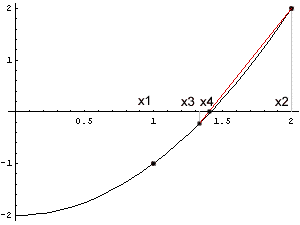
Beim Regula Falsi-Verfahren geht man ebenfalls von einem Intervall [x₁, x₂] aus, in dem die Funktion das Vorzeichen wechselt. Man ersetzt nun zwischen diesen zwei Werten f(x) durch eine lineare Funktion und berechnet deren Nullstelle. Mit anderen Worten: man verbindet die beiden Punkte durch eine Gerade und schneidet diese mit der x-Achse. Der neue Näherungswert x₃ wird im nächsten Schritt zur unteren oder oberen Intervallgrenze, je nachdem, ob f(x₃) negativ oder positiv ist. Dann wiederholt man die Berechnung.

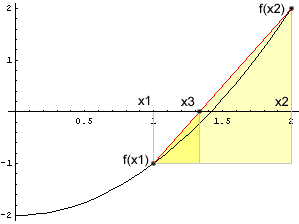
Die beiden gelben Dreiecke sind ähnlich, daher gilt:

Daraus erhalten wir:

oder (noch schöner, weil symmetrisch):

(Diese Formel entspricht genau der von Adam Ries verwendeten Rechenregel.)

Beispiel:

Die Tabelle zeigt die ersten Schritte der Berechnung von √2.

x1	x2		f(x3)
1	2	4/3 = 1,3333	-2/9 = -0,2222
4/3	2	7/5 = 1,4	-1/25 = -0,04
7/5	2	24/17 = 1,4128	-2/289 = -0,0069
24/17	2	41/29 = 1,4138	-1/841 = -0,0012
41/29	2	140/99 = 1,4141	-2/9801 = -0,0002

Hier haben wir also in 5 Schritten schon 3 richtige Dezimalstellen gefunden. Auch dieses Verfahren konvergiert garantiert, wenn f(x) im betrachteten Intervall stetig ist.

Sekantenverfahren

Man kann die Berechnung noch etwas beschleunigen, wenn man immer die letzten beiden Näherungwerte für den nächsten Schritt verwendet, ohne auf das Vorzeichen von f(x) zu achten:

x1	x2		f(x3)
1	2	4/3 = 1,3333	-2/9 = -0,2222
2	4/3	7/5 = 1,4	-1/25 = -0,04
4/3	7/5	58/41 = 1,4146	2/1681 = 0,0012
7/5	58/41	816/577 = 1,41421	-0,000006

Nach nur 4 Rechenschritten kennen wir also schon 5 richtige Dezimalstellen. Allerdings kann man bei dieser Methode auch Pech haben. Denn wenn bei einem Rechenschritt die Steigung der Sekante sehr klein ist, liegt der Schnittpunkt mit der x-Achse weit weg - man erhält also einen schlechteren Näherungswert. Wenn wir in unserem Beispiel mit den Startwerten x₁ = ³/₂, x₂ = -1 angefangen hätten, wäre x₃ = 1. Weil f(-1) = f(1) = -1 ist, wäre die nächste Sekante parallel zur x-Achse, und der nächste Rechenschritt wäre unmöglich.

Anwendung: Wärmeausdehnung von Eisenbahnschienen

Beim Verlegen von Eisenbahnschienen ließ man früher zwischen den einzelnen Schienenstücken einen kleinen Abstand, damit sich der Stahl bei Erwärmung ausdehnen konnte. Heute werden die Schienenabschnitte zu langen Strängen verschweißt und an den abgeschrägten Enden überlappend verlegt. Angenommen, ein 500 m langer, an den Enden fest verschraubter Schienenstrang dehnt sich um 6 cm aus. Wie hoch würde sich die Schiene in der Mitte wölben?

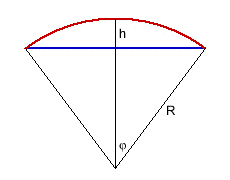
Wir nehmen der Einfachheit halber an, dass die verlängerte Schiene einen Kreisbogen bildet, und bezeichnen den halben Zentriwinkel mit φ. (Winkel werden hier, wie auch in den folgenden Beispielen, immer im Bogenmaß angegeben!) Die Länge des Kreisbogens beträgt dann 2R·φ = 500,06, und die Sehne ist 2R·sin(φ) = 500. Wenn wir R eliminieren und umformen, erhalten wir die Gleichung

500,06·sin(φ) - 500·φ = 0

Wir verwenden zur Lösung das Sekantenverfahren. Durch Probieren erhalten wir f(0,02) = 0,00053, f(0,03) = -0,00045. Daher nehmen wir 0,02 und 0,03 als Startwerte:

φ1	φ2	φ3	f(φ3)
0,02	0,03	0,02542	0,000156
0,03	0,02542	0,02660	0,000027
0,02542	0,02660	0,02685	-0,000002
0,02660	0,02685	0,02683	~ 0

Es ist also φ = 0,02683 = 1,537° und R = 500,06/2φ = 9318 m. Die Mitte des Kreisbogens befindet sich h = R(1 - cos(φ)) = 3,35 m über dem Boden!

(In Wirklichkeit sind die Schienen an jeder Schwelle fest angeschraubt. Durch die Wärmeausdehnung entstehen innere Spannungen, die von den Schwellen aufgenommen werden.)

Zurück - Weiter: Newtonsches Näherungsverfahren