Schritt für Schritt - Näherungsverfahren zum Lösen von Gleichungen

Intervallhalbierung
Regula Falsi und Sekantenverfahren
Newtonsches Näherungsverfahren
Fixpunktiteration

Wie berechnet man eigentlich √2? Wir wissen, dass das die positive Lösung der Gleichung x² - 2 = 0 ist und dass man diese Zahl nicht als Bruch oder endliche Dezimalzahl schreiben kann. Aber in der Praxis ist man schon zufrieden, wenn man das Ergebnis auf einige Dezimalstellen genau kennt (auch der Taschenrechner gibt ja nur einen Näherungswert an). Wie kann man eine solche Näherungslösung finden?

Die meisten Gleichungen, mit denen man in der Schule zu tun bekommt, sind exakt lösbar, das heißt, man kann die Lösungen durch die Grundrechnungsarten und Wurzelziehen finden. Aber bei Gleichungen 5. und höheren Grades gibt es im Allgemeinen keine exakte Lösung mehr, ebenso wenig wie bei transzendenten Gleichungen (also Gleichungen, bei denen Exponential- oder Winkelfunktionen vorkommen). Sogar eine so einfach aussehende Gleichung wie cos(x) = x lässt sich nur näherungsweise lösen. Solche Gleichungen treten bei praktischen Problemen oft auf. Im Lauf der Zeit hat man daher verschiedene Lösungsmethoden gefunden.

Jede Gleichung kann in der Form f(x) = 0 geschrieben werden. Es geht also darum, die Nullstelle(n) einer Funktion zu finden. Durch Probieren kann man einen Näherungswert finden, der in der Nähe der Nullstelle liegt, oder ein Intervall, in dem es eine Nullstelle liegen muss. Davon ausgehend, versucht man eine bessere Näherung oder ein kleines Intervall zu finden. Diese Berechnung wiederholt man dann so oft, bis man mit dem Ergebnis zufrieden ist (weil man z.B. schon eine bestimmte Anzahl an Dezimalstellen kennt oder f(x) kleiner als eine festgesetzte Schranke ist). Ein solches Verfahren heißt iterativ (von lat. itero, wiederholen). Wenn die Näherungswerte sich, wie gewünscht, der richtigen Lösung immer mehr annähern, sagt man, das Verfahren konvergiert. Man wiederholt die Berechnung so lange, bis man mit dem Ergebnis zufrieden ist. Ich werde die wichtigsten iterativen Verfahren vorstellen und an der Berechnung von √2 demonstrieren. Außerdem werde ich zu jeder Methode noch ein weiteres Anwendungsbeispiel vorstellen.

Intervallhalbierung (Bisektion)

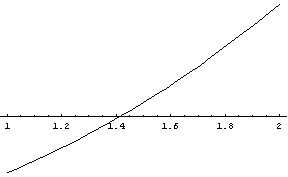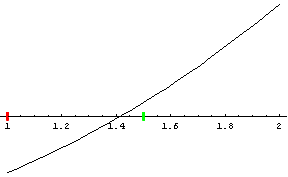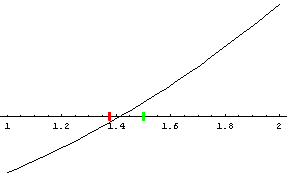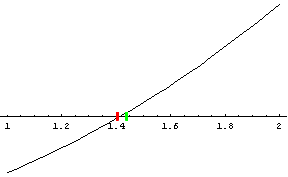
Wir suchen also die (positive) Nullstelle der Funktion f(x) = x² - 2. Wir können leicht feststellen, dass f(1) negativ, f(2) aber positiv ist. Die Lösung muss daher zwischen 1 und 2 liegen. Wir versuchen es mit dem arithmetischen Mittel ³/₂. f(³/₂) ist positiv, die Lösung liegt also zwischen 1 und ³/₂. Durch wiederholtes Halbieren können wir die Nullstelle in immer engere Grenzen einschließen. Die Mitte des Intervalls wird im nächsten Schritt zur unteren oder oberen Intervallgrenze, je nachdem, ob der Funktionswert dort negativ oder positiv ist.

x1	x2	x3 = (x1 + x2)/2	f(x3)
1	2	3/2 = 1,5	1/4 = 0,25
1	3/2	5/4 = 1,25	-7/16 = -0,4375
5/4	3/2	11/8 = 1,375	-7/64 = -0,1094
11/8	3/2	23/16 = 1,4375	17/256 = 0,0664
11/8	23/16	45/32 = 1,4063	-23/1024 = -0,0225

In 5 Schritten haben wir also nur eine Dezimalstelle von √2 gefunden. Nach 10 Schritten beträgt die Länge des Intervalls (1/2)¹⁰ ~ 0,0001; man braucht also jeweils 10 Rechenschritte, um 3 weitere Dezimalstellen zu bekommen. Das Verfahren konvergiert also sehr langsam und ist für die praktische Berechnung nicht so günstig. Andrerseits konvergiert es garantiert, wenn die Funktion f im untersuchten Intervall stetig ist. Denn nach dem Zwischenwertsatz hat jede stetige Funktion in einem abgeschlossenen Intervall mindestens eine Nullstelle, wenn die Funktionswerte an den Intervallgrenzen verschiedene Vorzeichen haben.

Das Bisektionsverfahren eignet sich auch sehr gut, um das Prinzip der Intervallschachtelung zu verstehen. Das ist eine Folge von Intervallen, die immer kleiner werden (die Länge geht gegen 0) und von denen jedes im vorigen enthalten ist. Es gibt dann genau eine Zahl, die in allen Intervallen enthalten ist. So kann man das Rechnen mit reellen Zahlen mathematisch sauber begründen.

"Anwendung": Wie man einen Löwen fängt

Man teilt die Wüste in zwei Hälften, in einer Hälfte ist der Löwe. Diese Hälfte teilt man wieder in zwei Hälften und so weiter. Irgendwann wird der Teil, in dem sich der Löwe befindet, so klein, dass er auf einem Bein stehen muss. Dann kann man ihn umstupsen und fangen :-)

Weiter: Regula Falsi