Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Bis jetzt haben wir nur Kegelschnitte in besonderen Lagen betrachtet - der Mittelpunkt, der Scheitel oder der Brennpunkt lag im Koordinatenursprung. Wir haben dabei immer Gleichungen 2. Grades in zwei Variablen erhalten.
Die allgemeine Gleichung 2. Grades in zwei Variablen können wir anschreiben als
ax² + 2bxy + cy² + 2dx + 2ey + f = 0 (*)
Man kann zeigen, dass es sich dabei immer um einen Kegelschnitt handelt, und zwar für
ac - b² > 0 eine Ellipse,
ac - b² = 0 eine Parabel und
ac - b² < 0 eine Hyperbel.
Allerdings kann der Kegelschnitt auch ausgeartet sein, also ein Punkt, eine Gerade oder ein Geradenpaar.
Ist d = e = 0, so handelt es sich um eine Ellipse oder Hyperbel in Mittelpunktslage.
Durch eine Hauptachsentransformation können wir den Kegelschnitt in Hauptlage bringen.
Dazu müssen wir das Koordinatensystem um einen Winkel φ drehen, wobei
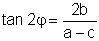. Die Gleichung in den neuen Koordinaten
x' und y' erhalten wir durch die Substitutionen
x = x' cos φ - y' sin φ
y = x' sin φ + y' cos φ
Die neue Gleichung ist dann von der Form
a'x'² + c'y'² + 2d'x' + 2e'y' + f' = 0
Das gemischte Glied xy ist weggefallen, wir haben also einen Kegelschnitt in achsenparalleler Lage. (Beachte, dass es für φ zwei Möglichkeiten gibt - eine führt zur 1., die andere zur 2. Hauptlage!)
Ist a' ≠ 0 und c' ≠ 0, handelt es sich um eine Ellipse oder Hyperbel. Diese können wir noch durch eine Verschiebung des Koordinatensystems in Hauptlage bringen, und zwar substituieren wirIst a' = 0 oder c' = 0, so stellt die Gleichung eine Parabel dar. Durch eine geeignete Verschiebung des Koordinatensystems können wir erreichen, dass der Scheitel im Koordinatenursprung liegt.
Beispiel: Wir betrachten die Kurve mit der Gleichung
xy = 1,also b = 1, a = c = d = e = 0, f = -1. tan 2φ ist nach der obigen Formel nicht definiert (etwas unexakt könnte man sagen, tan 2φ = ∞), daher ist 2φ = 90° und φ = 45°. (Wenn wir die Kurve zeichnen, sehen wir, dass es sich um eine um 45° gedrehte Hyperbel handelt.) Um die Gleichung in 1. Hauptlage zu bekommen, müssen wir also das Koordinatensystem um 45° drehen.
Durch die Substitution wird die Gleichung zu
Wir multiplizieren aus und schreiben der Einfachheit halber wieder x und y statt x' und y'. Das Ergebnis lautet
Es handelt sich also um eine gleichseitige Hyperbel mit den Halbachsen a = b = √2.
Wenn umgekehrt die Gleichung eines Kegelschnitts gesucht ist, der durch bestimmte Punkte gehen soll, müssen wir die Koordinaten dieser Punkte in die Gleichung (*) einsetzen und daraus die Unbekannten a bis f berechnen. Eine dieser Unbekannte können wir beliebig wählen, weil man ja die Gleichung mit einer beliebigen Konstanten multiplizieren kann. Es sind daher noch fünf unabhängige Unbekannte zu finden, und dazu brauchen wir fünf Gleichungen. Ein beliebiger Kegelschnitt ist also durch fünf Punkte eindeutig festgelegt.
