2. Die "klassische" Definition der Kegelschnitte

Die griechischen Mathematiker beschrieben Kurven durch ihre "charakteristischen Eigenschaften" oder "Symptome". Sie beschreiben dabei Beziehung zwischen der Abszisse (dem Abstand auf einer Grundlinie) und de Ordinate (dem Abstand normal zur Grundlinie, oder auch in einer anderen festgelegten Richtung). Das heißt, sie gingen ganz ähnlich vor, wie wenn wir heute eine Kurve in ein Koordinatensystem einzeichnen und eine Gleichung zwischen den Koordinaten aufstellen. Allerdings beschrieben sie diese Beziehungen meist durch Proportionen.

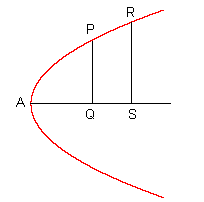	Betrachten wir zuerst die "charakteristische Eigenschaft" der Parabel: P und R seien zwei beliebige Punkte auf einer Parabel mit dem Scheitel A. Wir zeichnen die Ordinaten PQ und RS. Dann gilt: PQ² : RS² = AQ : AS das heißt, die Quadrate der Ordinaten verhalten sich zueinander wie die Abszissen, bzw. das Verhältnis PQ² : AQ hat für alle Parabelpunkte den selben Wert.
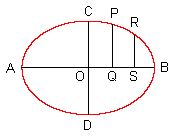	Für die Ellipse lautet die entsprechende Beziehung: PQ² : RS² = AQ·QB : AS·SB das heißt, die Quadrate der Ordinaten verhalten sich so wie die Produkte der Achsenabschnitte, oder das Verhältnis PQ² : AQ·QB ist konstant. Wenn wir den Nebenscheitel C betrachten, erhalten wir für dieses Verhältnis: PQ² : AQ·QB = CO² : AO²
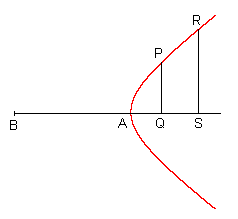	Auch für die Hyperbel gilt: PQ² : RS² = AQ·BQ : AS·BS Dabei liegen aber die Punkte Q und S in der Verlängerung der Achse. (Unter einer Hyperbel verstand man damals nur einen Hyperbelast. Die Beziehung gilt aber für den anderen Ast genauso.)

Der folgende Beweis (der auch übersprungen werden kann) folgt im Wesentlichen der Beweisidee von Apollonius. Ich habe ihn aber etwas vereinfacht. (Apollonius betrachtet ganz allgemein Schnitte an schiefen Kreiskegeln.)

Wir beweisen zuerst die Beziehung für die Parabel.

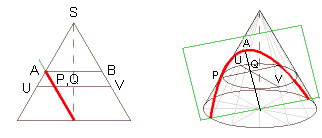
Wir schneiden einen Kegel so mit einer Ebene, dass wir eine Parabel erhalten. P sei ein beliebiger Punkt auf dieser Parabel. Nun müssen wir das Verhältnis 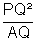berechnen.

Wir legen durch P eine horizontale Ebene, die den Kegel in einem Kreis schneidet. UV ist ein Durchmesser dieses Kreises und steht auf PQ normal. Dann gilt:

PQ² = UQ·QV (Höhensatz von Pythagoras)

Außerdem ist AQ = UA und QV = AB, und wegen des Strahlensatzes gilt: .

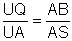Wir erhalten also für das gesuchte Verhältnis:

,

und das ist, wie behauptet, für alle Punkte der Parabel konstant.

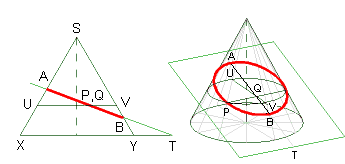
Für die Ellipse müssen wir unsere Figur noch etwas erweitern: wir verlängern die Achse der Ellipse bis zum Schnittpunkt mit der Basisebene des Kegels; diesen Schnittpunkt nennen wir T. Wir müssen jetzt das Verhältnis 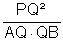bestimmen.

Wie vorhin gilt:

PQ² = UQ·QV

Aus dem Strahlensatz erhalten wir

und

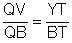
Wenn wir diese beiden Brüche miteinander multiplizieren, ergibt sich für das gesuchte Verhältnis:

,

und das ist wieder konstant.

Der Beweis für die Hyperbel geht ganz analog.

Inhalt - Zurück - Weiter: Mittelpunktsgleichung