Differentialrechnung

Der Differentialquotient

Problem: Wir suchen die Änderungsrate einer Funktion f an der Stelle x.
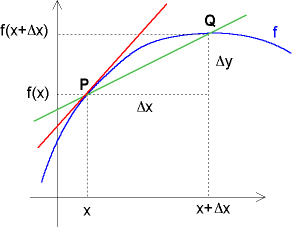
Geometrische Interpretation: Steigung der Tangente im Punkt P(x/f(x)).

Die Steigung der Sekante durch die Punkte P und Q (grün) beträgt

Diesen Ausdruck bezeichnet man als Differenzenquotient.

Nähert sich der Punkt Q dem Punkt P immer mehr, bis sie schließlich zusammenfallen, so geht die Sekante in die Tangente (rot) über.
Die Tangentensteigung ist also der Grenzwert der Sekantensteigung für
Dx ® 0 (lim = Limes = Grenzwert):

Das ist der sog. Differentialquotient. oder die Ableitung der Funktion f.

Schreibweisen: (sprich: "dy nach dx"), f'(x), y'

Zur Veranschaulichung siehe die Flash-Animation "Die Ableitung als Grenzwert" (mathe online) oder das Applet "Sekanten- und Tangentensteigung".

Beispiel:
Wir suchen die Steigung der Tangente an den Graphen der Funktion f(x) = x² im Punkt P(1/1).

Steigung der Sekante:

Wenn wir Dx gegen 0 gehen lassen, erhalten wir die Steigung der Tangente:
f'(1) = 2.

Wenn wir die Ableitung in einem beliebigen Punkt berechnen wollen, ersetzen wir in der Berechnung 1 durch x und erhalten:
f'(x) = 2x.

In der Praxis rechnet man nicht jedesmal den Differenzenquotienten aus, sondern benutzt die folgenden

Ableitungsregeln

Ableitung der wichtigsten Funktionen:

y = c (konstant)

y' = 0

y = xn

y' = n·xn-1

y = sin x

y' = cos x

y = cos x

y' = -sin x

y = ex

y = ex

y = ln x

Ableitungsregeln:

Konstantenregel

y = k· f(x)

y' = k· f'(x)

Summenregel

y = f(x) ± g(x)

y' = f'(x) ± g'(x)

Produktregel

y = f(x)·g(x)

y' = f'(x)·g(x) + f(x)·g'(x)

Quotientenregel

Kettenregel

y = f(g(x))

y' = f'(g(x))·g'(x)
("äußere Ableitung mal innere Ableitung")

Mit den markierten Regeln kann man bereits alle Polynomfunktionen differenzieren.

Beispiele:

y = 4x³ + 5x² - 3x + 2
y' = 4·3x² + 5·2x - 3·1 + 0 = 12x² + 10x - 3

  

 

 

y = (x² + 1)·sin x
y' = 2x· sin x + (x² + 1)· cos x

Produktregel:
f(x) = x² + 1, g(x) = sin x
f'(x) = 2x, g'(x) = cos x

Quotientenregel:
f(x) = x² - 1, g(x) = x² + 2
f'(x) = 2x, g'(x) = 2x

y = (x³ + 2)5
y' = 3x²·5(x³ + 2)4

Kettenregel:
f(x) = x³ + 2 = t, g(t) = t5
f'(x) = 3x², g'(t) = 5t4 = 5(x³ + 2)4

Lernziele:

  • Ich weiß, was die Ableitung einer Funktion bedeutet.
  • Ich kann Polynomfunktionen differenzieren.
  • Ich kenne die Ableitungen der wichtigsten Funktionen.
  • Ich kann Potenzregel, Quotientenregel und Kettenregel anwenden.

Übungen: Ableitungsregeln - Ableitung von Polynomfunktionen

Weitere Übungsbeispiele: http://www.zum.de/Faecher/M/NRW/pm/mathe/abl-bsp.htm.

Zum Inhaltsverzeichnis