Eine Funktion der Form
f: y = kx + d (k, d Î R)
heißt lineare Funktion.
Die Steigung der Geraden durch die Punkte P(x1/y1) und
Q(x2/y2) ist definiert durch
Δ - Delta - ist das Symbol für "Differenz".
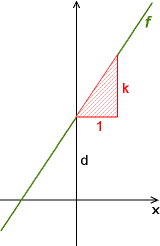
Man kann zeigen:
Der Graph einer linearen Funktion ist eine Gerade mit der Steigung k, die die y-Achse im Punkt (0/d) schneidet.
Daher kann man den Funktionsgraphen folgendermaßen zeichnen:
Sonderfälle:
Der Graph der Funktion
y = kx
(homogene lineare Funktion) ist eine Gerade durch den Koordinatenursprung mit der Steigung k.
Der Graph der Funktion
y = d
(konstante Funktion) ist eine Parallele zur x-Achse.
Lernziele:
|
Weiter: Quadratische Funktionen