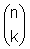. (Eine andere Schreibweise dafür ist C(n,k). Beachte, dass für n < k der
Binomialkoeffizient 0 ist.)Nr. 17 / Jänner 2007
In vielen Denkaufgaben geht es darum, eine Zahlenfolge fortzusetzen. Oft kann man das Bildungsgesetz finden, indem man sich die Differenzen zwischen den aufeinanderfolgenden Zahlen anschaut. Dabei erhält man wieder eine Folge, die sogenannte Differenzenfolge. Wir definieren:
Ist an eine Zahlenfolge, dann bezeichnen wir bn = an+1 - an als die dazugehörige Differenzenfolge.
Zuerst schauen wir uns ein ganz einfaches Beispiel an, die Folge der natürlichen Zahlen. Es ist also an = n. Dabei beginnen wir mit der Zählung bei 0:
an 0 1 2 3 4 5 ... n bn 1 1 1 1 1 ... 1
Die Differenzenfolge ist also konstant. Ein ähnliches Ergebnis erhalten wir für jede arithmetische Folge.
Als nächstes betrachten wir die Folge an = n². Diesmal berechnen wir auch die zweite Differenzenfolge cn, also die Differenzen der Differenzen:
an 0 1 4 9 16 25 ... n² bn 1 3 5 7 9 ... 2n + 1 cn 2 2 2 2 ... 2
Hier wird also erst die zweite Differenzenfolge konstant. Wie sieht es für an = n³ aus?
an 0 1 8 27 64 125 ... n³ bn 1 7 19 37 61 ... 3n² + 3n + 1 cn 6 12 18 24 ... 6n + 6 dn 6 6 6 ... 6
Die erste Differenzenfolge wird also durch ein quadratisches Polynom festgelegt, die zweite durch ein lineares, und die dritte
ist konstant. Allgemein kann man zeigen:
Wenn eine Folge durch ein Polynom k-ten Grades definiert wird, ist ihre k-te Differenzenfolge konstant gleich k!
(k Fakultät).
Jetzt sehen wir uns noch eine geometrische Folge an, nämlich an = 2n:
an 1 2 4 8 16 32 ... 2n bn 1 2 4 8 16 ... 2n cn 1 2 4 8 ... 2n
Hier stimmt die Differenzenfolge mit der ursprünglichen Folge überein. Wir können also beliebig oft die Differenzen bilden, ohne dass die Folge einfacher wird.
Können wir aus der Differenzenfolge die ursprüngliche Folge zurückgewinnen? Natürlich - wir müssen nur die bn addieren. Allerdings muss das erste Folgenglied angegeben sein. Es ist
b1 + b2 + ... bn = (a2 - a1) + (a3 - a2) + ... + (an+1 - an)
Wenn wir die Klammern auflösen, fallen die meisten Summanden weg, und wir erhalten
b1 + b2 + ... + bn = an+1 - a1, also
an+1 = a1 + b1 + b2 + ... + bn
Wir können genausogut an als Differenzenfolge auffassen und die dazugehörige Summenfolge sn berechnen: sn+1 = sn + an. Weil wir das erste Folgeglied beliebig wählen können, gibt es zu einer Folge unendlich viele Summenfolgen, die sich nur um eine Konstante unterscheiden.
Für die Folgen an = n² bzw. an = n³ erhalten wir z.B. die Summenfolgen (jeweils in der oberen Zeile):
sn 0 0 1 5 14 30 ... an 0 1 4 9 16 25 ...
sn 0 0 1 9 36 100 ... an 0 1 8 27 64 125 ...
Ich beginne jetzt wieder mit der Tabelle aus dem ersten Beispiel und schreibe darüber die Summenfolgen sn, tn, un usw. Als erste Zahl nehme ich immer 0.
un 0 0 0 0 1 5 15 ... tn 0 0 0 1 4 10 20 ... sn 0 0 1 3 6 10 15 ... an 0 1 2 3 4 5 6 ... bn 1 1 1 1 1 1 1 ...
Wenn man dieses Schema dreht, erkennt man das Pascal'sche Dreieck. Die erste Summenfolge besteht aus den Dreieckszahlen, die zweite aus den Tetraederzahlen usw. Allgemein stehen in der k-ten Zeile der Tabelle (von unten) die Binomialkoeffizienten
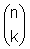. (Eine andere Schreibweise dafür ist C(n,k). Beachte, dass für n < k der
Binomialkoeffizient 0 ist.)
Aus dieser Tabelle hat Isaac Newton (1643 - 1727) eine Formel abgeleitet, mit deren Hilfe man das Bildungsgesetz einer Folge aus ihren Differenzenfolgen ermitteln kann:
Ein Beispiel: In wieviele Stücke kann man eine Torte mit n geraden Schnitten zerteilen? Die Stücke müssen nicht gleich groß sein, es ist also nicht nötig, dass alle Schnitte (wie sonst üblich) durch den Mittelpunkt gehen.
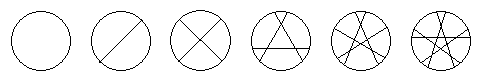
Wir zählen für n = 0 bis 5 die Stücke ab und stellen die Differenzenfolgen auf:
an 1 2 4 7 11 16 ... bn 1 2 3 4 5 ... cn 1 1 1 1 ...
Ab der nächsten Zeile sind alle Differenzen 0. Es ist also an = 1·C(n,0) + 1·C(n,1) + 1·C(n,2) = 1 + n + n(n-1)/2 = (n² + n + 2)/2.
Genauso erhält man jetzt die Formeln für die Summen der Quadratzahlen bzw. Kubikzahlen:
0² + 1² + 2² + ... + n² = (2n³ - 3n² + n)/6
0³ + 1³ + 2³ + ... + n³ = (n4 - 2n³ + n²)/4
(Das könnt ihr selbst nachrechnen.)
Schließlich betrachten wir noch eine fallende Zahlenfolge, nämlich die harmonische Folge an = 1/n. Nach unserer Definition würden wir lauter negative Differenzen erhalten. Daher ändern wir die Vorschrift ein bisschen ab in: bn = an - an+1. Außerdem beginnen wir jetzt mit der Zählung bei 1 (weil 1/0 nicht definiert ist):
an 1 1/2 1/3 1/4 1/5 1/6 ... 1/n bn 1/2 1/6 1/12 1/20 1/30 ... 1/[n(n+1)] cn 1/3 1/12 1/30 1/60 ... 2/[n(n+1)(n+2)] dn 1/4 1/20 1/30 ... 6/[n(n+1)(n+2)(n+3)]
Jetzt gilt: b1 + b2 + ... + bn = a1 - an+1. Die Folge an konvergiert aber gegen 0, genauso wie alle anderen Zeilen der Tabelle. Die Summe der unendlichen Reihe b1 + b2 + ... + bn + ... ist daher gleich a1:
1/2 + 1/6 + 1/12 + 1/20 + 1/30 + ... = 1
Dasselbe gilt auch für alle anderen Zeilen.
Gottfried Wilhelm Leibniz (1646 bis 1716) hat diese Folgen untersucht, als er seinen Differential- und Integralkalkül ausarbeitete. Er versuchte die Summe der reziproken Dreieckszahlen (also der Kehrwerte der Dreieckszahlen) zu berechnen. Hier könnt ihr nachlesen, dass er sich dabei auch einige Schnitzer erlaubt hat. Mit der obigen Tabelle geht es ganz einfach, denn diese Folge ist das Doppelte der Folge bn. Gleichzeitig erhält man Formeln für die Summe der reziproken Tetraederzahlen usw.
Wenn man die Tabelle dreht, erhält man das "Harmonische Dreieck":
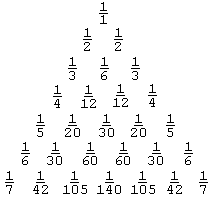
Es ist mit dem Pascal'schen Dreieck verwandt - die Zahlen in der n-ten Zeile sind die Kehrwerte der entsprechenden Zahlen des Pascal'schen Dreiecks, dividiert durch (n+1). Jede Zahl ist die Summe der beiden darunterliegenden Zahlen (statt wie bei Pascal der darüberliegenden). Auf http://www.cut-the-knot.org/Curriculum/Combinatorics/LeibnitzTriangle.shtml findet ihr noch einige nette Eigenschaften.
Was hat das alles mit Differential- und Integralrechnung zu tun? Wir können an auch als Funktion auffassen und die Punkte (n/an) in ein Koordinatenstem einzeichnen. bn ist dann die Steigung der Verbindungsstrecke aufeinanderfolgender Punkte. Das Bild zeigt den Graphen von an = n³:
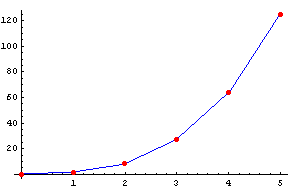
Für diese Folge haben wir als Differenzenfolge erhalten:
Wenn wir n vergrößern, heißt das, dass die Anzahl der Punkte zunimmt. Wir können aber den Maßstab so verändern, dass
das betrachtete Intervall immer gleich bleibt. Die Steigung sollte sich dann der Ableitung der Funktion annähern.
Tatsächlich hat die Funktion
Das Gleiche gilt für die anderen Folgen, die wir untersucht haben:
f(x) = x => f'(x) = 1
f(x) = x² => f'(x) = 2x.
Die k-te Differenzenfolge entspricht der k-ten Ableitung. Wenn man eine Polynomfunktion k-ten Grades k-mal differenziert,
erhält man eine konstante Funktion, nämlich
Die Differenzenfolge der harmonischen Folge war
f(x) = 1/x => f'(x) = -1/x²
Schließlich haben wir festgestellt, dass die Differenzenfolge einer geometrischen Folge wieder eine geometrische Folge
ist. Das entspricht der Tatsache, dass die Ableitung einer Exponentialfunktion wieder eine Exponentialfunktion ergibt.
Speziell ist
f(x) = ex => f'(x) = ex
Die Formel von Newton drückt die Glieder der ursprünglichen Folge durch die Anfangsglieder der Differenzenfolgen aus. Analog dazu kann man mit der Taylorreihe die Werte einer Funktion aus ihren Ableitungen an der Stelle x = 0 berechnen:
Die Summenfolge haben wir gebildet, indem wir die einzelnen Folgenglieder addiert haben. Man kann sich auch vorstellen,
dass man n Rechtecke der Höhe an und Breite 1 addiert. Wenn man n vergrößert, nähert sich dieser Wert der
Fläche unter dem Funktionsgraphen. Wir erhalten also so das Integral. Tatsächlich haben wir gefunden:
Die Summenfolge von an = n2 ist sn = (2n3 - 3n2 + n)/6 ~ n3/3,
und ∫x2dx = x3/3 ;
die Summenfolge von an = n3 ist sn = (n4 - 2n3 + n2)/4 ~ n4/4,
und ∫x3dx = x4/4.
So wie die Summenfolge ist auch das unbestimmte Integral nur bis auf eine Konstante festgelegt.
Wenn man die Summenfolge der harmonischen Folge bildet, erhält man die Harmonischen Zahlen:
Hn = 1 + 1/2 + 1/3 + ... + 1/n
Sie sind ungefähr so groß wie der natürliche Logarithmus von n:
Hn ~ ln n + 1/(2n) + γ.
(Die Zahl γ = 0,57721... bezeichnet man als Euler-Mascheronische Konstante.)
Bekanntlich ist ∫dx/x = ln x. Auch hier finden wir also einen Zusammenhang zur Integralrechnung.
Ich wünsche euch ein schönes und erfolgreiches Jahr 2007!
Jutta
Literatur: Conway, John H./Guy, Richard K.: Zahlenzauber. Von natürlichen, imaginären und anderen Zahlen, Basel 1997
(Kapitel 3: Differenzenfolgen, Kapitel 9: Harmonische Zahlen)
E-mail: gut.jutta.gerhard@chello.at
