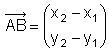
Im Allgemeinen legen wir Punkte in der Ebene durch ein rechtwinkeliges (kartesisches) Koordinatensystem fest. Die x-Koordinate (Abszisse) wird vom Ursprung aus nach rechts, die y-Koordinate (Ordinate) nach oben gemessen.
Andere Koordinatensysteme sind z.B. schiefwinkelige Koordinaten oder Polarkoordinaten.
Ausführliche Erklärung: http://www.mathe-online.at/mathint/zeich/i.html
Eine Strecke ist durch ihre Eckpunkte festgelegt, z.B. A(x1/y1), B(x2/y2). Eine gerichtete Strecke (einen Pfeil) kann man auch als Vektor schreiben:
("Endpunkt minus Anfangspunkt")
Wenn zwei Pfeile parallel und gleich lang sind, gehören sie zum selben Vektor.
(Mehr über Vektoren)
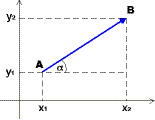
Die Länge einer Strecke erhalten wir nach dem Satz von Pythagoras:
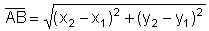
|
bzw. in Vektorschreibweise 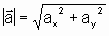
Die Steigung (der Anstieg) einer Strecke ist definiert durch
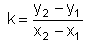
|
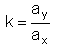
Für den Neigungswinkel der Strecke (das ist der Winkel, den sie mit der positiven x-Richtung einschließt) gilt:
| k = tan a |
Wir vereinbaren, dass wir immer den positiven Winkel zwischen 0° und 180° nehmen. Erhalten wir ein
negatives Ergebnis, müssen wir 180° addieren.
Falls x1 = x2, ist a = 90°.
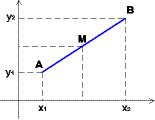
Der Halbierungspunkt der Strecke AB hat die Koordinaten
Beispiel:
Gegeben sind die Punkte A(1/1), B(5/4), C(-1/2) und D(3/5).
Die Vektoren AB und CD sind gleich: AB = CD =, daher bilden die Punkte ein Parallelogramm.
Die Länge der Strecke AB beträgt Ö(4²+3²) = 5, der Anstieg k = 3/4 = 0,75 und der Neigungswinkel a = tan-1(0,75) = 36,9°.
Der Halbierungspunkt der Strecke AB hat die Koordinaten MAB(3/2,5).
Wie wir wissen, ist die Lösungsmenge einer linearen Gleichung mit zwei Unbekannten eine Gerade, d.h., alle Punkte, deren Koordinaten die Gleichung erfüllen, liegen auf einer Geraden (siehe Gleichungen mit mehreren Unbekannten). Wir bezeichnen diese Gleichung daher als Normalform der Geradengleichung:
| ax + by = c |
Sonderfälle:
Wir können diese Gleichung (außer im letzten Fall) zur Gleichung einer linearen Funktion umformen, der Hauptform der Geradengleichung:
| y = kx + d |
k ist dabei die Steigung der Geraden (siehe lineare Funktionen). Den Neigungswinkel erhält man wie oben.
Ist von einer Geraden die Steigung k und ein Punkt P(x1/y1) bekannt, können wir die Gleichung auch in der Punkt-Steigungs-Form angeben:
bzw.
| y - y1 = k·(x - x1) |
Beispiel:
Im obigen Beispiel lautet die Gleichung der Geraden durch A und B:
g: y - 1 = 0,75·(x - 1) bzw.
g: y = 0,75x + 0,25
Den Schnittpunkt zweier Geraden erhalten wir, indem wir das entsprechende Gleichungssystem lösen.
Der Winkel, den die Geraden mit den Neigungswinkeln a1
und a2 einschließen, beträgt
j = a2 - a1.
Hier kommt es - im Unterschied zum Neigungswinkel einer Strecke - nicht auf das Vorzeichen an.
Allerdings ist auch der Winkel 180° - j möglich. Im Zweifelsfall
sollte zur Kontrolle eine Zeichnung gemacht werden.
Beispiel:
Wie wir gesehen haben, hat die Gerade durch A und B den Neigungswinkel a1 = 36,9°.
Die Gerade durch A und C hat die Steigung -0,5 und den Neigungswinkel a2 = 153,4°.
Die beiden Geraden schließen also den Winkel j = 153,4° - 36,9° = 116,5° bzw. 180° - 116,5° = 63,5° ein.
Parallele Geraden haben dieselbe Steigung.
Stehen zwei Geraden mit den Steigungen k1 und k2 normal aufeinander, so gilt
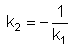
|
bzw. k1·k2 = -1
Beispiel:
Gesucht ist die Gleichung der Streckensymmetrale von AB. Sie geht durch den Halbierungspunkt MAB und steht auf AB normal, hat also die Steigung -4/3. Die Gleichung lautet also:
m: y - 2,5 = -4/3·(x - 3) bzw.
m: y = -4x/3 +6,5
Lernziele:
|
Weiter: Kreis