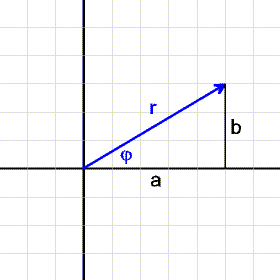
Man kann eine komplexe Zahl auch durch ihren Betrag |z| (Abstand vom Nullpunkt) und ihr Argument φ (Winkel, den sie mit der x-Achse einschließt) angeben:

|
|
a = r·cos φ b = r·sin φ |
Wir können daher auch schreiben:
(Man vereinbart meist, dass φ zwischen 0° und 360° liegen soll. Weil die Umkehrung der Tangensfunktion nicht eindeutig ist, sollte man bei der Berechnung von φ immer eine Skizze machen!)
Die Multiplikation und Division von komplexen Zahlen ist in der Polardarstellung ziemlich einfach. Die Multiplikation mit (r; φ) entspricht nämlich einer Streckung um den Faktor r mit einer gleichzeitigen Drehung um den Winkel φ. Mit anderen Worten: wenn man zwei komplexe Zahlen multipliziert, werden die Beträge multipliziert und die Winkel addiert; bei einer Division werden die Beträge dividiert und die Winkel subtrahiert.
(r1; φ1)·(r2; φ2) = (r1·r2; φ1 + φ2)
(r; φ)n = (rn; n·φ)
Die letzte Gleichung schreibt man oft in anderer Form (Formel von de Moivre):
[r·(cos φ + i·sin φ)]n = rn·(cos nφ + i·sin nφ)
Die Regeln für das Wurzelziehen sind analog, aber Achtung:
Wenn man zum Argument einer komplexen Zahl ein Vielfaches von 360° addiert, ändert sich die Zahl nicht.
Wenn man zum Argument von z ein Vielfaches von 360°/n addiert, ändert sich zn nicht.
Für n√z gibt es daher n verschiedene Möglichkeiten:
(k = 0, 1, ..., n-1)
Im Reellen gilt:
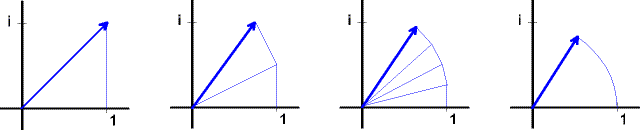
Die ersten drei Bilder zeigen 1 + i, (1 + i/2)2 und (1 + i/4)4. Wie man sieht, nähert sich der Streckenzug immer mehr einem Kreisbogen der Länge 1 an (viertes Bild). Es ist also ei = cos 1 + i·sin 1. (Der Winkel ist dabei im Bogenmaß angegeben!) Man kann zeigen, dass allgemein die Eulersche Formel gilt:
eiφ = cos φ + i·sin φ (φ im Bogenmaß)
Die Polardarstellung einer komplexen Zahl wird daher zu
Setzt man φ = π (= 180°), so erhält man die bemerkenswerte Gleichung
eiπ = -1
Geschichte der komplexen Zahlen
Eine Anwendung der komplexen Zahlen: Komplexe Wechselstromrechnung