Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch

Das Imaginäre wird real

Die Geschichte der komplexen Zahlen

Die Entdeckung
Die "mystische" Periode
Die komplexe Zahlenebene
Wozu komplexe Zahlen?

Die Entdeckung

Wenn man in der Schule zum ersten Mal mit Quadratwurzeln zu tun hat, lernt man, dass man aus einer negativen Zahl nicht die Wurzel ziehen kann. Denn das Quadrat einer reellen Zahl - ob positiv oder negativ - ist immer positiv. In der Oberstufe erfährt man dann, dass es doch auch Quadratwurzeln aus negativen Zahlen gibt, aber diese Wurzeln sind nicht reell, sondern gehören zu einer anderen Art von Zahlen, die man "imaginär" oder "komplex" nennt. Was können wir uns unter diesen Zahlen vorstellen, und wie sind die Mathematiker auf die Idee gekommen, sich mit ihnen zu beschäftigen?

Der erste, der mit diesem Gedanken spielte, war Girolamo Cardano (1501 - 1576). In einem der letzten Kapitel seiner "Ars magna" (seinem Hauptwerk über das Lösen von Gleichungen) behandelt er Gleichungen, in denen negative Zahlen auftreten. Er schreibt:

Wenn jemand sagt: teile 10 in zwei Teile, deren Produkt (...) 40 ist, so ist klar, dass dieser Fall unmöglich ist. Desungeachtet wollen wir wie folgt verfahren: Wir teilen 10 in zwei gleiche Teile, von denen jeder 5 ist. Diese quadrieren wir, das macht 25. Wenn du willst, subtrahiere 40 von den gerade erhaltenen 25 (...); der damit erhaltene Rest ist -15, die Quadratwurzel daraus, addiert zu oder subtrahiert von 5 gibt die beiden Teile mit dem Produkt 40. Diese sind also 5 + √-15 und 5 - √-15.

Was Cardano hier in Worten ausdrückt, ist die bekannte Lösungsformel für quadratische Gleichungen; mit ihr erhält man für die Gleichung x(10 - x) = 40 die Lösungen x1,2 = 5 ± √-15. Ohne sich vorerst darum zu kümmern, welche Art von "Zahlen" das sein sollen, rechnet er nach, dass ihre Summe 10 und ihr Produkt 40 ist (weil die Wurzeln wegfallen). Er hat also schon eine Idee davon gehabt, dass man auch mit Wurzeln aus negativen Zahlen rechnen könnte; allerdings bezeichnet er diese Zahlen als "quantitas sophistica", spitzfindige Größen, und hält sie für unnütze Spielereien.

Ein Nachfolger von Cardano war der Ingenieur Rafael Bombelli (1526 – 1572). Er legte im Auftrag des Kirchenstaats Sümpfe trocken. In seiner Freizeit beschäftigte er sich mit Algebra. Er schrieb ein Lehrbuch (erschienen 1572), dass einfacher als Cardanos "Ars magna" und auch für Nichtmathematiker verständlich sein sollte. Darin untersuchte er auch die Gleichung

x³ = 15x + 4

Mit der Cardano'schen Lösungsmethode erhält man dafür die Lösung

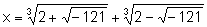
Andrerseits kann man leicht nachrechnen, dass x = 4 eine Lösung der Gleichung ist. Es ist also möglich, mit dieser anscheinend sinnlosen Formel ein sinnvolles Ergebnis zu erzielen! Bombelli versuchte daher, mit diesen seltsamen Wurzeln weiterzurechnen. Er entdeckte, dass (2 + √-1)³ = 2 + 11·√-1 = 2 + √-121, also x = 2 + √-1 + 2 - √-1 = 4. (Die anderen zwei Lösungen sind übrigens -2 + √3 und -2 - √3. Dieser Fall, der "casus irreducibilis", tritt immer dann auf, wenn eine kubische Gleichung 3 verschiedene reelle Lösungen hat.)

Bombelli erkannte, dass er eine neue Art von Wurzeln entdeckt hatte, mit denen sich sinnvoll rechnen ließ. Er betrachtete sie als eine Art Vorzeichen und nannte sie "più di meno" ("plus von minus", in heutiger Schreibweise +i) und "meno di meno" ("minus von minus" bzw. -i). Analog zu den Rechenregeln für negative Zahlen gab er auch für diese Zahlen Regeln an:

"plus" mal "plus von minus" ist "plus von minus" (+1·+i = +i)
"minus" mal "plus von minus" ist "minus von minus" (-1·+i = -i)
"plus" mal "minus von minus" ist "minus von minus" (+1·-i = -i)
"minus" mal "minus von minus" ist "plus von minus" (-1·-i = +i)
"plus von minus" mal "plus von minus" ist "minus" (+i·+i = -1)
"plus von minus" mal "minus von minus" ist "plus" (+i·-i = +1)
"minus von minus" mal "plus von minus" ist "plus" (-i·+i = +1)
"minus von minus" mal "minus von minus" ist "minus" (-i·-i = -1)

Diese Art zu rechnen war natürlich völlig ungewohnt - in einer Zeit, in der man sogar negative Zahlen noch sehr skeptisch betrachtete. Aber ein erster Schritt war getan.

Weiter: Die "mystische" Periode