Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Wozu komplexe Zahlen?
Die komplexen Zahlen haben sich heute einen fixen Platz in der Mathematik und Physik erobert. Es geht längst nicht mehr nur darum, dass die Anzahl der Lösungen einer Gleichung "stimmt". Viele Theorien nehmen eine einfachere Gestalt an, wenn man sie von der höheren Warte der komplexen Zahlen aus betrachtet.
Die trigonometrischen Funktionen beispielsweise bilden innerhalb der reellen Funktionen anscheinend eine ganz eigene Klasse. Aber wenn man die Eulersche Formel umformt, erhält man die Beziehungen
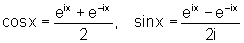
Auch mit den Hyperbelfunktionen sind sie eng verknüpft, und zwar durch die Gleichungen
cosh x = cos ix, sinh x = -i sin ix
Die Analogien zwischen Winkel- und Hyperbelfunktionen sind also nicht nur zufällig. Aus der Sicht der komplexen Zahlen bilden also Exponentialfunktion, trigonometrische und Hyperbelfunktionen eine einzige Familie von Funktionen.
Bei der Untersuchung von harmonischen Schwingungen tritt die Differentialgleichung
y'' = k·yauf. Wenn man im Bereich der reellen Zahlen bleiben will, muss man zwei Fälle unterscheiden, je nachdem ob k positiv oder negativ ist. Im ersten Fall braucht man Exponentialfunktionen für die Lösung, im zweiten Fall trigonometrische Funktionen. Aber wenn man komplexe Zahlen einbezieht, fällt diese Unterscheidung weg. Man kann dann alle diese Gleichungen auf dieselbe Art lösen. Die imaginären Anteile fallen im Lauf der Rechnung weg, und das Ergebnis ist wieder reell.
Auch in der Elektrotechnik benutzt man komplexe Zahlen. Bei einem Wechselstrom können zum Beispiel die Spannung und die Stromstärke durch Sinuskurven dargestellt werden. Wenn eine Spule in den Stromkreis eingefügt wird, ändert sich nicht nur die Stromstärke, sondern auch ihre Phase - das heißt, die Stromstärke erreicht ihr Maximum etwas später als die Spannung, sie hinkt sozusagen hinter der Spannung nach. Bei einem Kondensator läuft sie der Spannung voraus. Diese Phasenverschiebungen können wesentlich einfacher berechnet werden, wenn man alle auftretenden Größen - Spannung, Stromstärke und Widerstand - als komplexe Zahlen betrachtet. (Die Elektrotechniker nennen die imaginäre Einheit j, um Verwechslungen mit der Stromstärke I zu vermeiden. Mehr zu dem Thema siehe hier.)
Ein letztes Beispiel: In jedem Feld, das sich im Gleichgewicht befindet (zum Beispiel eine Strömung in einer Flüssigkeit, ein elektrostatisches oder ein Magnetfeld), gilt die sogenannte Laplacegleichung. Wenn die betreffende Größe nur von zwei Dimensionen abhängt (etwa eine Strömung parallel zur x-y-Ebene), kann man sie durch eine komplexe Funktion ausdrücken. Dadurch werden die Berechnungen wesentlich vereinfacht.
Diese Beispiele haben (hoffentlich) gezeigt, dass die komplexen Zahlen nicht nur eine Gedankenpielerei einiger Mathematiker sind. Sie sind aus den modernen Naturwissenschaften nicht mehr wegzudenken, weil sie sich in vielen Gebieten ausgezeichnet zur Beschreibung der Wirklichkeit eignen - oft sogar besser als die reellen Zahlen. Daher kann man mit Recht sagen, dass sie genauso "real" sind wie die positiven und negativen Zahlen.
Literatur und Links
Gericke, Helmut: Mathematik in Antike und Orient. Wiesbaden 2003
Alten, H.-W. u. a.: 4000 Jahre Algebra. Berlin 2003
Wessel, Caspar: On Directiones analytiske Betegning. Kopenhagen 1799
Französische Übersetzung: Essai sur la représentation analytique de la direction.
Copenhague 1897
Argand, Robert: Essai sur une manière de représenter les quantités imaginaires dans les constructions géometriques. Paris (?) 1874
Gauß, Carl Friedrich: Theoria residuorum biquadraticorum. 1831
Die Arbeiten von Wessel und Argand (französich) finden sich auf der Homepage der Französischen Nationalbibliothek (http://gallica.bnf.fr/), der Aufsatz von Gauß (lateinisch) im Göttinger Digtalisierungszentrum (http://gdz.sub.uni-goettingen.de/en/index.html, letzter Eintrag unter "Gauss").
Maor, Eli: Die Zahl e - Geschichte und Geschichten. Basel 1996
(Im 14. Kapitel werden komplexe Zahlen behandelt - von dort stammt der Titel dieses Artikels.)