Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Die "mystische" Periode
In den folgenden zwei Jahrhunderten gewöhnten sich die Mathematiker langsam daran, mit diesen Zahlen zu rechnen. Sie wußten zwar noch nicht genau, was sie sich darunter vorstellen sollten, aber sie brauchten sie für die Theorie der algebraischen Gleichungen. René Descartes (1667 - 1754) vermutete, dass eine Gleichung immer so viele Lösungen hat, wie ihr Grad angibt (wenn man die mehrfachen Lösungen entsprechend oft zählt). Allerdings sind diese Lösungen nicht immer reell, sondern manchmal "seulement imaginaires", nur vorgestellt. Daher kommt die Bezeichnung "imaginäre Zahlen". (Die Vermutung ist als "Fundamentalsatz der Algebra" bekannt; sie wurde von Gauß bewiesen.)
Gottfried Wilhelm Leibniz (1646 - 1716) entdeckte die Beziehung
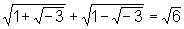
und war davon äußerst beeindruckt. In einem Brief an den Physiker Pierre Varignon (2. Februar 1702) berichtet er von seiner Entdeckung und schreibt: "Als ich den verstorbenen Herrn H... darauf aufmerksam machte, erwiederte er mir, es läge darin etwas für uns unbegreifliches." (Mit H... ist Christian Huygens gemeint.) Leibniz selbst nennt √-1 "ein Wunder der Analysis, ein Monstrum der idealen Welt, fast ein Amphibium zwischen Sein und Nichtsein". Wie man sieht, waren damals auch Mathematiker noch ziemlich mystisch veranlagt :-)
Man entdeckte auch andere interessante Zusammenhänge. François Viète (1540 - 1603) hatte folgende Regel angegeben, um Sinus und Cosinus der Vielfache eines Winkels zu finden (in heutiger Schreibweise):
Berechne (cos α + sin α)n nach der binomischen Formel. Verteile die Glieder abwechselnd auf zwei Zeilen und setze in jeder Zeile das erste Glied als positiv, das zweite als negativ usw. Die erste Zeile ergibt cos (nα), die zweite sin (nα).
Ein Beispiel:
(cos α + sin α)³ = cos³ α + 3 cos² α sin α + 3 cos α sin² α + sin³ α
cos (3α) = cos³ α - 3 cos α sin² α
sin (3α) = 3 cos² α sin α - sin³ α.
Abraham de Moivre (1667 - 1754) entdeckte nun, dass man diese Beziehung viel leichter ausdrücken kann, wenn man imaginäre Zahlen verwendet. Dann erhält man die nach ihm benannte Formel (wieder in moderner Schreibweise):
cos (nα) + i sin (nα) = (cos α + i sin α)n
Die Bezeichnung "i" für die imaginäre Einheit stammt übrigens von Leonhard Euler (1707 - 1783). Er hat sie aber nicht konsequent benutzt. Allgemein verbreitet wurde sie erst durch Gauß.
Euler entdeckte eine andere wichtige Beziehung. Er untersuchte die Potenzreihenentwicklung verschiedener Funktionen. Es war damals schon bekannt, dass man viele wichtige Funktionen als Grenzwerte von unendlichen Reihen berechnen kann, z.B.
Euler setzte nun in die Potenzreihe für ex den Wert ix statt x ein. Als er die einzelnen Glieder berechnete (i² = -1, i³ = -i, ...) und jeweils die reellen und imaginären Glieder zusammenfasste, erhielt er die überraschende Gleichung
eix = cos x + i sin x
Strenggenommen müsste man vorher beweisen, dass die einzelnen Schritte erlaubt sind,
das heißt, dass sich der Grenzwert der Reihe nicht ändert, wenn man die Reihenfolge der
einzelnen Glieder ändert. Aber Euler ersetzte die mathematische Strenge, die man
heute fordern müsste, oft durch einen sicheren Instinkt. Außerdem lässt sich seine Formel
auch durch eine andere Überlegung motivieren, für die man keine Reihen braucht.
Die Formel von de Moivre kann man nämlich umschreiben zu
Wenn man in der Eulerschen Formel x = π setzt, erhält man die Beziehung
eiπ = -1,
die viele Mathematiker für die schönste aller Formeln halten.
In den Formeln von de Moivre und Euler deutet sich schon eine Beziehung zwischen den imaginären Zahlen und der Trigonometrie an. Die Mathematiker hatten die geometrische Interpretation der komplexen Zahlen schon vor ihrer Nase liegen - aber es dauerte lange, bis sie sie erkannten.