Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
|
Brüche und KreiseWas haben diese Bilder mit Bruchrechnen zu tun? |
|
Leute, die im Bruchrechnen ungeübt sind, addieren manchmal so: 1/3 + 1/2 = 2/5. Sie wenden die "Regel" an: "Zähler plus Zähler, Nenner plus Nenner". Das ist natürlich falsch. 2/5 liegt zwischen 1/3 und 1/2, kann also auf keinen Fall die Summe sein. (An dieser Stelle bin ich im Kurs immer nahe daran, in Verzweiflung auszubrechen.)
Aber man kann dieses Ergebnis trotzdem sinnvoll interpretieren. Angenommen, in einem Gefäß wird 1 Liter Orangensaft mit Wasser auf 3 Liter verdünnt, in einem anderer Gefäß verdünnt man 1 Liter Saft auf 2 Liter. Der Saftanteil beträgt also im ersten Fall 1/3, im zweiten 1/2. Wenn man die beiden Lösungen zusammenschüttet, beträgt der Saftanteil des Gemischs 2/5. Wir erhalten mit dieser Rechenoperation also eine Art Mittelwert, den man als Mediant bezeichnet. Man kann leicht nachrechnen, dass der Mediant zweier positiver Brüche immer dazwischen liegt (d.h. aus 0 < a/b < c/d folgt a/b < (a+c)/(b+d) < c/d).
Leider hat die Sache einen Schönheitsfehler. Die Darstellung eines Bruches ist bekanntlich nicht eindeutig - man kann ihn ja beliebig erweitern. Wir hätten also auch rechnen können: (2+1)/(6+2) = 3/8 oder (4+3)/(12+6) = 7/18 ... Bei solchen Mischungsaufgaben kann man ja auch jede beliebige Konzentration erhalten, solange sie zwischen den Konzentrationen der Ausgangsprodukte liegt. Wir wollen uns daher auf gekürzte Brüche beschränken und definieren:
Der Mediant zweier positiver, gekürzter Brücheund
ist der Bruch
.
Unter einer Farey-Reihe oder Farey-Folge versteht man alle echten Brüche (also Brüche < 1), deren Nenner nicht größer als eine bestimmte Zahl ist, der Größe nach geordnet. So lautet zum Beispiel die 5. Farey-Reihe F5:
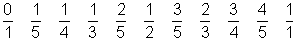
Diese Reihen haben einige interessante Eigenschaften:
In einer Farey-Reihe ist jeder Bruch der Mediant seiner Nachbarbrüche.
So ist z.B. 1/5 = (0+1)/(1+4), 1/4 = (1+1)/(5+3), 1/3 = (1+2)/(4+5), ... Diese Eigenschaft ist dem englischen Geologen John Farey (1766 - 1826) aufgefallen, der sie 1816 in einem Brief an die Zeitschrift Philosophical Magazine veröffentlichte. Deswegen tragen diese Reihen seinen Namen, obwohl diese Tatsache schon 1802 von einem gewissen C. Haros erwähnt wurde. Bewiesen wurde sie von Augustin Louis Cauchy (1789 - 1857).
Dadurch erhalten wir eine Möglichkeit, Farey-Reihen zu konstruieren, ohne dass wir mühsam alle Brüche der Größe nach ordnen müssen. Wir beginnen mit der ersten Farey-Reihe F1: 0/1, 1/1. In der n-ten Reihe schreiben wir zwischen je zwei Brüche ihren Medianten, wenn dessen Nenner n ist. Wir erhalten so nacheinander die Reihen
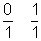
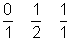
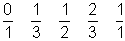
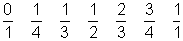
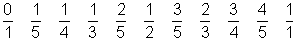
und so weiter. Wenn man in jedem Schritt alle Medianten anschreibt, egal wie groß ihr Nenner ist, erhält man einen sogenannten Stern-Brocot-Baum. In ihm taucht jeder echte Bruch genau einmal auf. Und wenn man in der ersten Reihe noch den symbolischen Bruch 1/0 dazuschreibt, erhält man alle positiven rationalen Zahlen (die rechte Hälfte des Baumes enthält die Kehrwerte der Brüche in der linken Hälfte).
Wenn 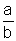 und
und 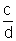 zwei aufeinanderfolgende
Glieder einer Farey-Reihe sind, ist bd - ac = 1.
zwei aufeinanderfolgende
Glieder einer Farey-Reihe sind, ist bd - ac = 1.
Beweis:
Die Aussage gilt offenbar für F1, denn 1·1 - 0·1 = 1.
Wenn sie für zwei Brüche a/b und c/d gilt, vererbt sie sich auch auf ihren Medianten:
b(a+c) - a(b+d) = ab + bc - ab - ad = bc - ad = 1
Genauso zeigt man: (b+d)c - (a+c)d = 1.
Daraus folgt, dass die Differenz zweier aufeinanderfolgender Farey-Brüche 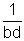 beträgt.
beträgt.
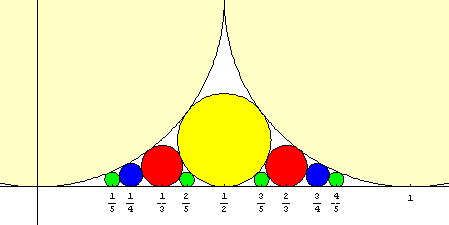
Der amerikanischer Mathematiker Lester R. Ford (1886 - 1975) fand eine äußerst ansprechende Möglichkeit, Farey-Reihen graphisch darzustellen. Er zeichnete über jedem Punkt der Zahlengeraden, der einem Bruch p/q entspricht, einen Kreis mit dem Durchmesser 1/q². Diese Kreise schneiden einander nie, aber sie berühren einander oft, und zwar genau dann, wenn ihre Berührungspunkte aufeinanderfolgenden Farey-Brüchen entsprechen. (Auf dem Bild sieht man die Kreise, die zu F5 gehören.)
|
|
Beweis:
Wir leiten zuerst eine allgemeine Bedingung dafür ab, dass zwei Kreise einander und eine Gerade berühren. Aus dem rechtwinkeligen Dreieck (linkes Bild) lesen wir ab:
s² = (r1 + r2)² - (r1 - r2)² = 4r1r2
Dabei ist s der Abstand zwischen den Berührpunkten, r1 und r2 sind die Kreisradien.
Wenn die beiden Kreise zu aufeinanderfolgenden Farey-Brüchen gehören, ist
,
was zu zeigen war.
Wenn wir noch einen dritten Kreis konstruieren, der die anderen beiden und die Gerade berührt (rechtes Bild), muss gelten: s1 + s2 = s. Das kann man umformen zu
(*).
Diese Aufgabe ist ein Spezialfall eines Problems, das der griechische Geometer Apollonius von Perge (ca. 262 - 190 v. Chr.) behandelt hat: Gesucht ist ein Kreis, der drei gegebene Objekte (Punkte, Geraden oder Kreise) berührt. Wenn man einen Punkt als Kreis mir Radius 0 und eine Gerade als Kreis mit Radius unendlich betrachtet, kann man das Problem einfacher formulieren:
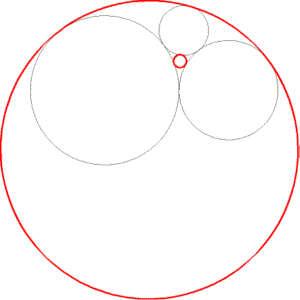
Gesucht ist ein Kreis, der drei gegebene Kreise berührt.
Dafür gibt es im Allgemeinen bis zu acht verschiedene Lösungen (zwei Kreise können einander von außen oder von innen berühren). Wenn die drei gegebenen Kreise einander aber auch gegenseitig berühren, gibt es nur mehr zwei Möglichkeiten (die beiden roten Kreise im Bild).
René Descartes (1596 - 1650) fand eine elegante Bedingung dafür dass von vier Kreisen jeder die anderen drei berührt. Er benutzte in seiner Formel nicht die Radien der Kreise, sondern deren Kehrwerte, die Krümmungen k1 bis k4:
(k1 + k2 + k3 + k4)² = 2(k1² + k2² + k3² + k4²)
Wenn ein Kreis die anderen von außen berührt, gibt man der Krümmung ein negatives Vorzeichen. Eine Gerade hat die Krümmung 0. (In diesem Fall erhält man aus der Formel nach einigen Umformungen die Gleichung (*).)
Wenn man in der Descartes'schen Kreisformel eine Variable, z.B. k4, als Unbekannte betrachtet, erhält man eine
quadratische Gleichung mit zwei Lösungen. Wenn man eine Lösung kennt, kann man aus dem Satz von Vieta sofort die
andere berechnen, denn es gilt:
Eine "apollonische Kette" |
Diese Packung entsteht aus dem Quadrupel |
Der englische Chemiker Frederick Soddy (1877 - 1956), der für die Entdeckung der Isotope 1921 den Nobelpreis bekommen hatte, fand die Descartes'sche Kreisformel neu und verallgemeinerte sie auf 3 Dimensionen. Wenn von fünf Kugeln jede die vier anderen berührt, gilt für ihre Krümmungen:
(k1 + k2 + k3 + k4 + k5)² = 3(k1² + k2² + k3² + k4² + k5²)
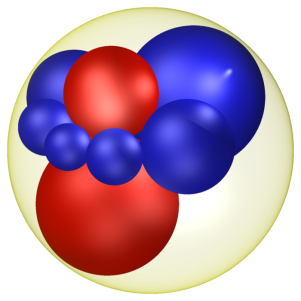
Wenn drei Kugeln einander berühren, kann man einen Kranz von sechs weiteren Kugeln um sie legen. Soddy bewies, dass sich der Ring immer schließt. Eine solche Figur nennt man "Soddy's Hexlet".
Soddy veröffentlichte seine Entdeckung 1936 in der Zeitschrift Nature im Form eines Gedichtes. Weil man auf englisch von "küssenden" Kreisen und Kugeln spricht, trägt es den romantischen Titel
The Kiss Precise
For pairs of lips to kiss maybe
Involves no trigonometry.
'Tis not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance from the center.
Though their intrigue left Euclid dumb
There's now no need for rule of thumb.
Since zero bend's a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum.To spy out spherical affairs
An oscular surveyor
Might find the task laborious,
The sphere is much the gayer,
And now besides the pair of pairs
A fifth sphere in the kissing shares.
Yet, signs and zero as before,
For each to kiss the other four
The square of the sum of all five bends
Is thrice the sum of their squares.
Literatur und Links
Conway, John H./Guy, Richard K.: Zahlenzauber. Von natürlichen, imaginären und anderen Zahlen. Basel 1997 (Kapitel 6)
Pöppe, Christoph: Kreispackungen. In: Spektrum der Wissenschaft, Dossier 2/08, S. 49
Pöppe, Christoph: Die Getriebe des Teufels. Ebd., S. 68
Hier findet man viele schöne Bilder von Kreispackungen:
http://www.ams.org/featurecolumn/archive/kissing.html
(englisch) und
http://pagesperso-orange.fr/math-a-mater/pack/packingcircle.htm
(französisch),
und hier von Kugelpackungen:
http://pagesperso-orange.fr/math-a-mater/pack/packing.htm
(französisch).