Exkurs: Kurven in Parameterdarstellung

Viele Kurven kann man durch eine einzige Gleichung beschreiben, z.B. die Parabel (y = x²) oder den Kreis (x² + y² = r²). Bei anderen ist das nicht möglich, aber die Koordinaten können als Funktion einer weiteren Variable t, des sogenannten Parameters angegeben werden:

x = x(t), y = y(t)

(Man kann sich zum Beispiel vorstellen, dass die Kurve durch die Bewegung eines Punktes entsteht. x(t) und y(t) sind dann die Koordinaten des Punktes zum Zeitpunkt t.)

Nach einer Schreibweise, die Newton eingeführt hat, bezeichnet man die Ableitungen 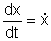und 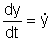. Ebenso sind 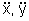die zweiten Ableitungen.

Die Fläche, die von einer Kurve eingeschlossen wird, berechnet man nach der Formel

,

die Bogenlänge ist

Um eine Kurve zu beschreiben, wollen die Mathematiker auch die Richtung und die Krümmung an einem bestimmten Punkt wissen. Die Richtung ist durch den Tangentialvektor 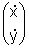gegeben. Die Krümmung wird durch den Krümmungskreis bestimmt, das ist der Kreis, der sich im gegebenen Punkt besonders gut an die Kurve anschmiegt. Er hat den Radius

,

und die Koordinaten des Mittelpunkts lauten

Die Krümmung selbst ist definiert als 1/r, der Kehrwert des Krümmungsradius.

Die Menge der Mittelpunkte aller Krümmungskreise ergibt eine neue Kurve, die Evolute der Kurve.

Zurück