Die Würfelverdopplung mit der Kissoide

Bei diesem Problem geht es darum, zu einem gegebenen Würfel einen mit dem doppelten Volumen zu finden. Wenn a die Seitenlänge des Würfels ist, muss man also die Strecke a·³√2 konstruieren. Das ist gleichbedeutend damit, zu zwei Strecken a und b zwei mittlere Proportionalen zu finden, also zwei Strecken x und y, so dass a : x = x : y = y : b. Setzt man b = 2a, so ist x die gesuchte Lösung.

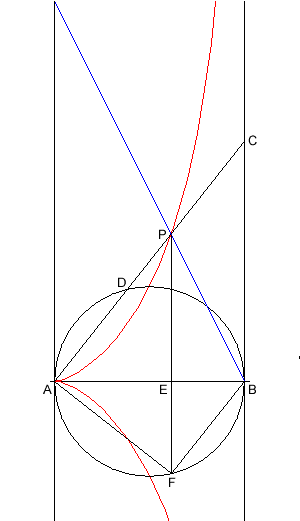
Wir konstruieren eine Kissoide, wie angegeben, und eine Gerade durch B mit der Steigung 2 (blau). Sie schneidet die Kurve in P. Wir zeichnen die Verbindungsgerade AP und erhalten die Punkte C und D. Außerdem legen wir durch P eine Senkrechte, die den Kreisdurchmesser in E und den unteren Halbkreis in F schneidet.

Der Winkel AFB ist ein rechter Winkel (Thaleskreis.) Wegen der Konstruktionsvorschrift liegt F am Kreis genau gegenüber von D. Daher ist auch FAD ein rechter Winkel, und die Geraden AP und BF sind parallel. Die Dreiecke BEF, FEA und AEP sind also alle ähnlich zueinander, und es gilt:

BE : EF = EF : AE = AE : PE

Wir haben also zu den Strecken BE und PE = 2·BE zwei mittlere Proportionalen gefunden, und in allen drei Dreiecken verhalten sich die Katheten wie 1 : ³√2. Wenn wir das Dreieck AEP vergrößern, sehen wir, dass auch AB : BC = 1 : ³√2. Wir haben also zur Strecke a = AB die ³√2-fache Strecke konstruiert.

Hier ist noch ein analytischer Beweis: Die Gleichung der Kissoide lautet

(1)     y²(a - x) = x³

und die Gerade durch B hat die Gleichung

(2)     y = 2a - 2x = 2(a - x).

Wenn wir (1) mit 2 multiplizieren und (2) einsetzen, erhalten wir für die Koordinaten des Schnittpunktes P

y³ = 2x³, also y = x·³√2.

Zurück