Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Ich möchte jetzt einige ausgewählte Kurven dritten Grades vorstellen. Viele von ihnen sind nach den Mathematikern benannt, die sie entdeckt oder als erster untersucht haben. Die Gleichungen sind jeweils in Koordinaten- und in Parameterform angegeben. Je nachdem, wie man die Kurve ins Koordinatensystem legt, sind verschiedene Gleichungen möglich - daher unterscheiden sie sich oft von den vorhin angegebenen Normalformen.
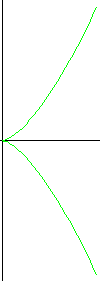
Die Neilesche (semikubische) Parabel
|
y² = x³ x = t², y = t³ |
Diese Kurve, eine divergierende Parabel, war eine der ersten, deren Länge man bestimmen konnte. Heute berechnet man die Bogenlänge
einer Kurve mit Hilfe der Integralrechnung, und zwar nach der Formel 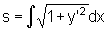 .
Dabei ergeben sich meist ziemlich komplizierte Ausdrücke (für die Ellipse und die Hyperbel kann man
z.B. das Integral nur näherungsweise berechnen). In diesem Fall kann man aber eine ziemlich einfache
Substitution durchführen und erhält das Ergebnis:
.
Dabei ergeben sich meist ziemlich komplizierte Ausdrücke (für die Ellipse und die Hyperbel kann man
z.B. das Integral nur näherungsweise berechnen). In diesem Fall kann man aber eine ziemlich einfache
Substitution durchführen und erhält das Ergebnis:
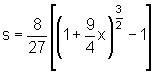
William Neile (1637 - 1670), ein englischer Mathematiker und Astronom, fand dieses Ergebnis 1657, also noch vor der Erfindung der Integralrechnung. Er zeigte geometrisch, dass die Kurvenlänge proportional zur Fläche einer Parabel ist.
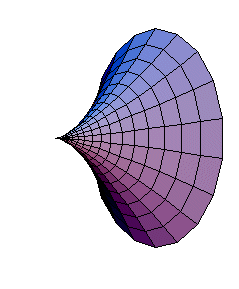
Wenn die Neilesche Parabel um die x-Achse rotiert, entsteht ein Körper, den ich Neilescher Kegel nennen möchte (rechts). Er wird uns später noch einmal begegnen.
Tschirnhausens Kubik
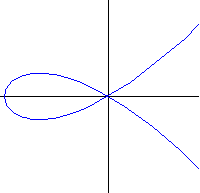
|
3ay² = x²(x + a) x = a(3t² - 1), y = at(3t² - 1) |
Auch hier handelt es sich um eine divergierende Parabel. Für den Parameterwert t = ±1/√3 ergibt sich beide Male der Punkt (0/0); die Kurve hat also dort einen Doppelpunkt. Der Umfang der Schlinge beträgt u = 4a√3/3 und der Flächeninhalt A = 8a²√3/45.
Ehrenfried Walter von Tschirnhaus (1651 - 1708) war ein bedeutender deutscher Wissenschaftler des 17 Jahrhunderts. Er arbeitete unter anderem mit Leibniz zusammen und war auch an der Erfindung des Porzellans beteiligt. Die nach ihm benannte Kurve wurde später auch von de L'Hôpital und Catalan untersucht.
Ich möchte die Kurve "Alpha-Parabel" nennen - in Erinnerung an meine Schulzeit, als ein paar Klassenkollegen und ich eine solche Kurve suchten. Wir fanden damals keine Lösung, weil wir nur Kegelschnitte, aber keine kubischen Kurven kannten.
Die Kissoide (Efeukurve) des Diokles
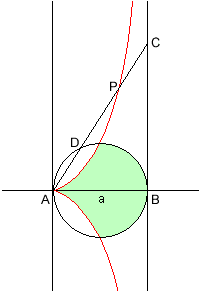
|
y²(a - x) = x³
|
Der griechische Mathematiker Diokles (ca. 240 - 180 v. Chr.) fand diese Kurve, als er versuchte, das Problem der Verdopplung des Würfels zu lösen. Sie wird so konstruiert: Zeichne einen Kreis mit dem Durchmesser AB = a und die Tangente in B. Eine beliebige Gerade durch A schneidet die Tangente in C und den Kreis in D. Bestimme den Punkt P auf der Geraden so, dass AP = DC. Wenn sich die Gerade um A dreht, beschreibt P eine Kissoide.
Die Kurve hat die Gerade x = a als Asymptote, sie ist also eine defiziente Hyperbel. Diokles nannte sie "Efeukurve", weil ihn die Fläche zwischen Kurve und Kreis an ein Efeublatt erinnerte. Wie er damit den Würfel verdoppelte, könnt ihr hier nachlesen.
Christiaan Huygens (1629 - 1695) schaffte es, auf geometrischem Weg die Fläche zwischen der Kurve und ihrer Asymptote zu bestimmen. Sie beträgt A = 3a²π/4, das ist drei mal der Flächeninhalt des erzeugenden Kreises.
Newton erfand ein Gerät, mit dem man die Kissoide und andere Kurven zeichnen kann (siehe http://www.museo.unimo.it/labmat/Smnewtin.htm).
Man kann die Kissoide auch definieren durchdie Beziehung AC·PC = a². Ersetzt man die rechte Seite durch eine andere (positive oder negative) Konstante, so erhält man eine Familie von Kurven, die als Sluzesche Kubik bekannt sind (siehe vorige Seite, Bild zu "defiziente Hyperbel"). Ein Spezialfall davon (AC·PC = 4a²) ist die
Trisectrix von MacLaurin
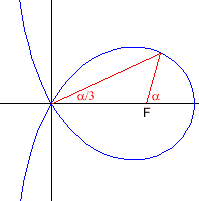
|
y²(a + x) = x²(3a - x) |
Die Gleichung sieht ein wenig anders aus, weil ich die Kurve um 180° gedreht habe. In dieser Lage hat die Kurve die Asymptote x = -a, der Durchmesser der Schlinge ist 3a. Der Punkt F(2a/0) heißt Brennpunkt der Trisectrix.
Colin MacLaurin (1698 - 1746) wurde mit 19 Jahren Mathematikprofessor in Aberdeen (Schottland), später in Edinburgh. Er verbreitete die Theorien Newtons, die damals noch ganz neu waren. Mit der Trisectrix löste er das Problem der Dreiteilung des Winkels (daher der Name "Dreiteilende"). Zeichnet man nämlich im Brennpunkt eine beliebigen Winkel α ein und verbindet den Schnittpunkt mit der Kurve mit dem Kreuzungspunkt, so erhält man dort den Winkel α/3.
Wenn man die Trisectrix ein wenig staucht und um 45° dreht, ergibt sich eine weitere berühmte Kurve:
Das kartesische Blatt
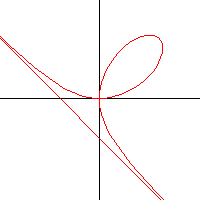
|
x³ + y³ - 3axy = 0
|
Die Asymptote dieser Kurve hat die Gleichung x + y + a = 0. Der Flächeninhalt der Schlinge beträgt 3a²/2, das ist genauso groß wie die Fläche zwischen Kurve und Asymptote.
René Descartes (1596 - 1650) untersuchte die Kurve mit der von ihm erfundenen Koordinatenmethode. Allerdings rechnet er noch nicht mit negativen Koordinaten, und so war er der Meinung, dass das "Folium" aus vier gleichen Schlingen besteht.
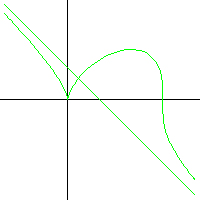
Der Kreis zweiter Ordnung
|
x³ + y³ = ax²
|
Um den seltsamen Namen dieser Kurve zu erklären, muss ich etwas ausholen. Die Gleichung eines Kreises
mit Durchmesser a und Mittelpunkt auf der x-Achse, der durch den Koordinatenursprung geht, kann man auch so schreiben:
x : y = y : (a - x).
Die linke Seite dieser Gleichung kann man abwandeln zu
xn : yn = y : (a - x).
Eine solche Kurve wird manchmal als "Kreis n-ter Ordnung" bezeichnet. Wenn man n = 2 setzt und ein bisschen umformt,
erhält man die angegebene Gleichung.
Auch diese Kurve gehört zu den defizienten Hyperbeln. Sie hat eine Spitze bei (0/0) und eine Asymptote mit der Gleichung x + y = a/3.
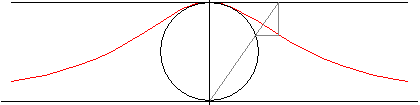
Die Versiera (Lockenkurve) der Agnesi
|
y(x² + a²) = a³
|
Bei dieser Kurve handelt es sich um eine parabolische Hyperbel mit nur einer Asymptote. Um sie zu konstruieren, zeichnet man einen Kreis durch den Koordinatenursprung mit Durchmesser a, der Mittelpunkt liegt auf der y-Achse. Dann legt man eine beliebige Gerade durch den Koordinatenursprung. Vom Schnittpunkt mit dem Kreis zieht man eine waagrechte Linie, vom Schnittpunkt mit der Geraden y = a eine Senkrechte. Der Schnittpunkt dieser beiden Linien ergibt einen Kurvenpunkt.
Die Kurve erinnert an die Gaußsche Glockenkurve, darf aber nicht mit ihr verwechselt werden (die Glockenkurve ist transzendent)! Die Fläche zwischen der Kurve und der x-Achse hat den Inhalt A = a²π, ist also vier mal so groß wie der erzeugende Kreis.
Maria Gaetana Agnesi (1718 - 1799) war die Tochter eines reichen Mailänder Kaufmanns. Als junges Mädchen war sie wegen ihrer außergewöhnlichen Intelligenz und Bildung berühmt. Später wollte sie ein ein Kloster eintreten. Auf die Bitten ihres Vaters blieb sie aber doch in seinem Haushalt und kümmerte sich um die Erziehung ihrer 20(!) jüngeren Geschwister. Für ihre Brüder schrieb sie die "Instituzioni analitiche", ein Lehrbuch der Differentialrechnung, die damals noch nicht sehr verbreitet war. In diesem Buch untersuchte sie auch die Lockenkurve, die daher nach ihr benannt wurde. Durch einen dummen Übersetzungsfehler (Verwechslung von "versiera" mit "avversiera", Hexe) heißt sie im englischen Sprachraum "witch of Agnesi".
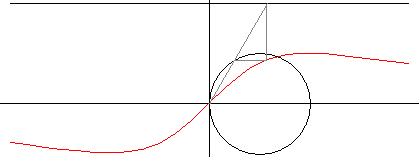
Die Anguinea (Schlangenkurve)
|
y(x² + a²) = a²x
|
Wenn man die selbe Konstruktion mit einem Kreis durchführt, dessen Mittelpunkt auf der x-Achse liegt, erhält man die Schlangenkurve (engl. serpentine). Diese Art, eine Kurve zu erzeugen, bezeichnet man als Hyperbolismus: man geht von einer beliebigen Kurve aus (hier von einem Kreis) und ersetzt jeden Punkt (x,y) durch den Punkt (ax/y,x). Wie Newton feststellt, sind alle kubischen Kurven mit a = b = 0 Hyperbolismen von Kegelschnitten. (Gegenüber der Darstellung von Newton sind hier x- und y-Achse vertauscht.)
Zurück - Weiter: Analogien zwischen Kegelschnitten und Kurven dritten Grades