Analogien zwischen Kegelschnitten und Kurven dritten Grades

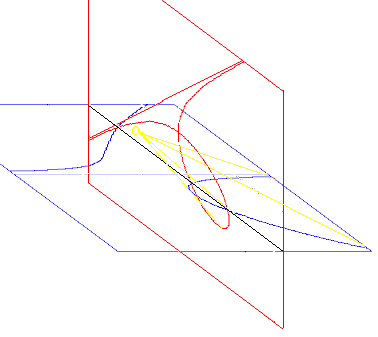Newton hat die kubischen Kurven nicht nur analog zu Kegelschnitten benannt (Hyperbel, Parabel ...), sondern auch eine Reihe von weiteren Parallelen entdeckt. Am interessantesten finde ich, wie man eine Kurve aus einer anderen durch Zentralprojektion erhalten kann. Man kann sich das als Schatten vorstellen, den eine Kurve auf eine andere Ebene wirft, wenn sie von einer punktförmigen Lichtquelle beleuchtet wird. Allerdings werden auch die Punkte hinter der Lampe projiziert. Das Bild zeigt, wie ein Kartesisches Blatt aus dem Projektionszentrum O auf einen Dreizack abgebildet wird.

Bekanntlich sind alle Kegelschnitte Projektionen eines Kreises (dabei entsteht ja ein Lichtkegel). Newton fand heraus, dass man alle Kurven dritten Grades als Projektion einer der fünf divergierenden Parabeln darstellen kann.

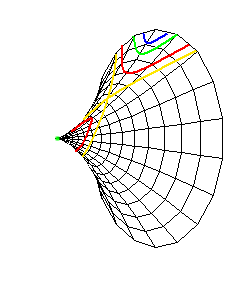Diese fünf Parabeln erhält man, wie Newtons Übersetzer Christopher R. M. Talbot in seinem Kommentar feststellt, als ebene Schnitte eines Neileschen Kegels - je nachdem, ob die Schnittebene an der Spitze des Kegels vorbeigeht (blau), sie enthält (grün), ein Stück von ihr abschneidet (rot) oder die Oberfläche des Kegels von innen berührt (gelb). (Wenn die Schnittebene durch die Kegelachse geht, entsteht natürlich die ursprüngliche Neilesche Parabel.) Die ganze Vielfalt der Kurven dritten Grades lässt sich also auf einige wenige Grundformen zurückfüren.

Einige weitere Analogien:

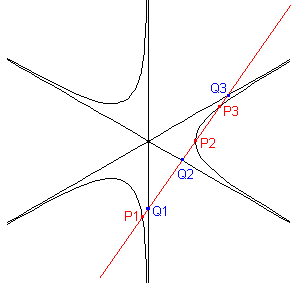Angenommen, eine Gerade schneidet die Kurve in den Punkten P₁, P₂, P₃ und die Asymptoten in den Punkten Q₁, Q₂, Q₃. Dann ist P₁Q₁ + P₂Q₂ + P₃Q₃ = 0. (Hier sind immer gerichtete Strecken gemeint, das heißt, wenn zwei Strecken verschiedene Richtungen haben, bekommt eine von ihnen eine negatives Vorzeichen.)

Das entspricht dem Satz, dass beim Schnitt einer Hyperbel mit einer Geraden die Abschnitte zwischen Hyperbel und Asymptoten gleich lang sind.

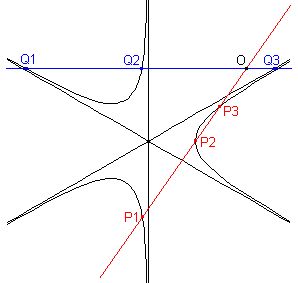Legt man durch einen Punkt O zwei Geraden, die die Kurve in P₁, P₂, P₃ bzw. Q₁, Q₂, Q₃ schneiden, dann hängt das Verhältnis (OP₁·OP₂·OP₃) : (OQ₁·OQ₂·OQ₃) nur von der Richtung der Geraden ab (egal wo der Punkt O liegt).

Das entspricht dem Sehnensatz bei Kegelschnitten.

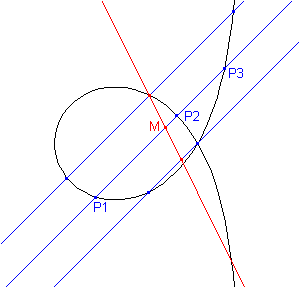Eine Gerade schneidet die Kurve in den Punkten P₁, P₂, P₃. Der Punkt M sei der "Mittelpunkt" der drei Schnittpunkte, das heißt, MP₁ + MP₂ + MP₃ = 0. Wenn die Gerade parallel verschoben wird, beschreibt der Punkt M eine Gerade.

Diese Eigenschaft ist analog zu konjugierten Richtungen bei Kegelschnitten.

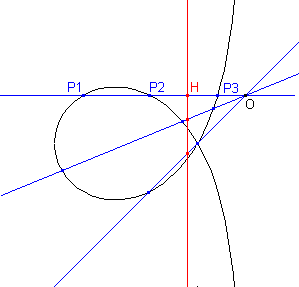Und noch einmal schneidet eine Gerade durch O die Kurve in den Punkten P₁, P₂, P₃. Wir bestimmen den Punkt H auf der Geraden so, dass OH das harmonische Mittel von OP₁, OP₂ und OP₃ ist. Wenn sich die Gerade um O dreht, bewegt sich H auf einer Geraden.

Diese Beziehung ist analog zur Pol-Polare-Beziehung bei Kegelschnitten. Sie wurde nicht von Newton entdeckt, sondern von seinem Mitarbeiter Roger Cotes (1682-1716), dem Herausgeber von Newtons Hauptwerk "Principia". Ein Beweis findet sich auf http://www.mathpages.com/home/kmath192/kmath192.htm.

Zurück - Weiter: Eine bemerkenswerte Raumkurve