Der Horopter - eine bemerkenswerte Raumkurve

Zum Abschluss wollen wir einen kleinen Ausflug in den dreidimensionalen Raum unternehmen. Eine Raumkurve wird am besten in Parameterform angegeben. Man kann sie aber auch als Schnitt zweier Flächen beschreiben, also durch zwei Gleichungen in drei Variablen. Eine Kurve n-ten Grades erkennt man daran, dass sie eine Ebene in maximal n Punkten schneidet.

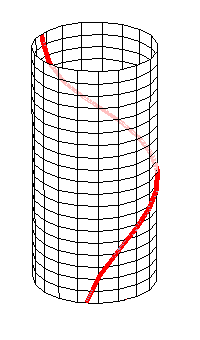
Eine der einfachsten kubischen Raumkurven ist die sogenannte Horopterkurve:

Man kann sich vorstellen, dass man einen Ast der Tangenskurve auf einen Papierstreifen malt und diesen zu einem Zylinder zusammenrollt. Die Gleichung sieht auf den ersten Blick nicht algebraisch aus; man kann aber x und y durch z ausdrücken:

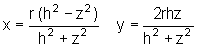
Außerdem kann man die Kurve auf verschiedene Arten als Schnitt zweier Flächen darstellen, zum Beispiel eines Zylinders (x² + y² = r²) und eines schiefen Kreiskegels (h(x-r)² + hy² - 2ryz = 0).

Der Name "Horopter" (griech. "Sehgrenze") kommt aus der Optik. Er bezeichnet alle Punkte, deren Bilder in beiden Augen auf einander entsprechende Punkte der Netzhaut abgebildet werden. Wenn man geradeaus schaut, besteht er aus einem horizontalen Kreis (wie auf http://www.psychologie.uni-heidelberg.de/ae/allg/lehre/wct/w/w6_raum/w640_binokulare_tk.htm erklärt wird) und einer vertikalen Geraden durch den Fixationspunkt. Schaut man in eine andere Richtung, so wird daraus unsere Kurve.

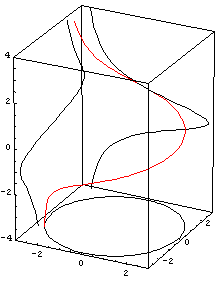Der Grundriss des Horopters, also seine Parallelprojektion auf die x-y-Ebene, ist ein Kreis. Aus diesem Grund heißt er auch "kubischer Kreis". Bei allen anderen Projektionsrichtungen erhält man verschiedene Kurven dritten Grades. Die Projektion auf die x-z-Ebene ist eine Lockenkurve und das Bild auf der y-z-Ebene eine Schlangenkurve.

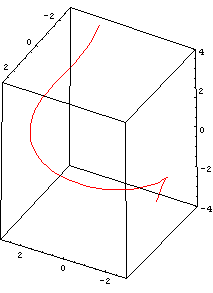Und wenn man die Kurve aus einer bestimmten Richtung anschaut, sieht man einen Kreis zweiter Ordnung. Wenn man in die dritte Dimension geht, entdeckt man also noch mehr Zusammenhänge zwischen den verschiedenen Kurventypen, die in der Ebene nicht auffallen.

Zurück

Literatur und Links

Sir Isaac Newton's Enumeration of lines of the third order ..., übers. v. C.R.M. Talbot, London 1860
http://name.umdl.umich.edu/ABQ9451.0001.001 (englisch)

Euler L., Introductio in analysin infinitorum, Band 2, 1748
(Im Internet habe ich leider nur eine französische Übersetzung gefunden: http://gallica.bnf.fr/ark:/12148/bpt6k38858)

Scriba C. J. / Schreiber P., 5000 Jahre Geometrie, Berlin 2001

Jahnke H. N. (Hrsg.), Geschichte der Analysis, Heidelberg 1999

Famous Curves Index (University of St Andrews, Scotland): http://www-history.mcs.st-and.ac.uk/~history/Curves/Curves.html (englisch)

A Visual Dictionary of Special Plane Curves (Xah Lee): http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html (englisch)

Encyclopédie des Formes mathématiques remarquables: http://www.mathcurve.com/ (französisch)

Homepage von Dr. Dörte Haftendorn: http://www.mathematik-verstehen.de
Viele interessante Informationen unter "Kurven, Analytische Geometrie"